Elektrische Schwingungen und Funkwellen

Navigationshilfe

Diese Navigationshilfe zeigt die ersten Schritte zur Verwendung der Präsention. Sie kann mit ⟶ (Pfeiltaste rechts) übersprungen werden.

Navigation

Zwischen den Folien und Abschnitten kann man mittels der Pfeiltasten hin- und herspringen, dazu kann man auch die Pfeiltasten am Computer nutzen.

Navigationspfeile für die Präsentation

Weitere Funktionen

Mit ein paar Tastenkürzeln können weitere Funktionen aufgerufen werden. Die wichtigsten sind:

F1
Help / Hilfe
o
Overview / Übersicht aller Folien
s
Speaker View / Referentenansicht
f
Full Screen / Vollbildmodus
b
Break, Black, Pause / Ausblenden der Präsentation
Alt-Click
In die Folie hin- oder herauszoomen

Übersicht

Die Präsentation ist zweidimensional aufgebaut. Dadurch sind in Spalten die einzelnen Abschnitte eines Kapitels und in den Reihen die Folien zu den Abschnitten.

Tippt man ein „o“ ein, bekommt man eine Übersicht über alle Folien des jeweiligen Kapitels. Das hilft sich zunächst einen Überblick zu verschaffen oder sich zu orientieren, wenn man das Gefühlt hat sich „verlaufen“ zu haben. Die Navigation erfolgt über die Pfeiltasten.

Referentenansicht

Referentenansicht

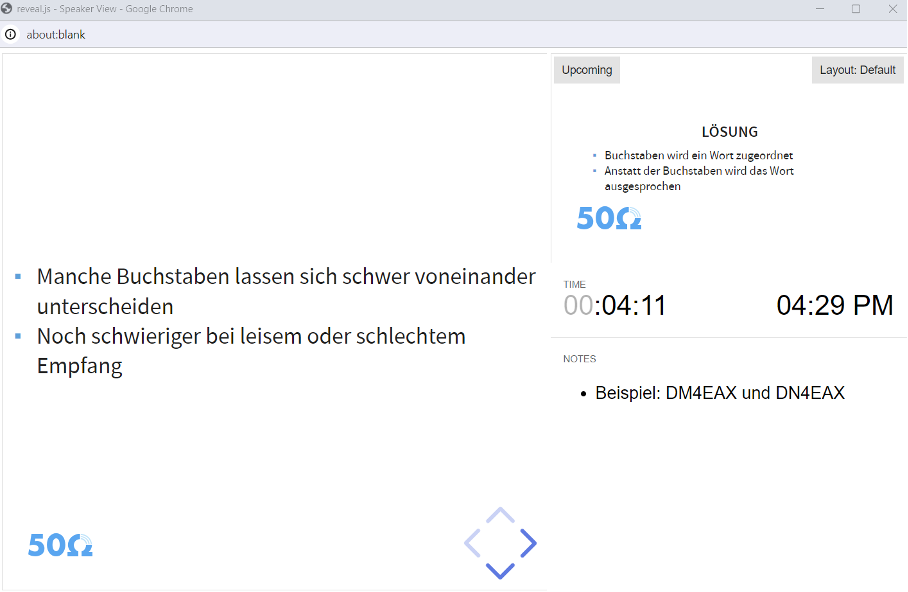
Tippt man ein „s“ ein, bekommt man ein neues Fenster, die Referentenansicht.

Indem man „Layout“ auswählt, kann man zwischen verschieden Anordnungen der Elemente auswählen.

Praxistipps zur Referentenansicht

  • Wenn man mit einem Projektor arbeitet, stellt man im Betriebssystem die Nutzung von 2 Monitoren ein: Die Referentenansicht wird dann zum Beispiel auf dem Laptop angezeigt, während die Teilnehmer die Präsentation angezeigt bekommen.
  • Bei einer Online-Präsentation, wie beispielsweise auf TREFF.darc.de präsentiert man den Browser-Tab und navigiert im „Speaker View“ Fenster.
  • Die Referentenansicht bezieht sich immer auf ein Kapitel. Am Ende des Kapitels muss sie geschlossen werden, um im neuen Kapitel eine neue Referentenansicht zu öffnen.
  • Um mit dem Mauszeiger etwas zu markieren oder den Zoom zu verwenden, muss mit der Maus auf den Bildschirm mit der Präsentation gewechselt werden.

Vollbild

Tippt man ein „f“ ein, wird die aktuelle Folie im Vollbild angezeigt. Mit „Esc“ kann man diesen wieder verlassen.

Das ist insbesondere für den Bildschirm mit der Präsentation für das Publikum praktisch.

Ausblenden

Tippt man ein „b“ ein, wird die Präsentation ausgeblendet.

Sie kann wie folgte wieder eingeblendet werden:

  • Durch klicken in das Fenster.
  • Durch nochmaliges Drücken von „b“.
  • Durch klicken der Schaltfläche „Resume presentation:
Schaltfläche für Resume Presentation

Zoom

Bei gedrückter Alt-Taste und einem Mausklick in der Präsentation wird in diesen Teil hineingezoomt. Das ist praktisch, um Details von Schaltungen hervorzuheben. Durh einen nochmaligen Mausklick zusammen mit Alt wird wieder herausgezoomt.

Das Zoomen funktioniert nur im ausgewählten Fenster. Die Referentenansicht ist hier nicht mit dem Präsenationsansicht gesynct.

Zehnerpotenzen

Große und kleine Werte

  • Im Amateurfunk haben wir große und kleine Werte
  • Um sich viele 0-en zu sparen, wurde bereits mit Einheitenvorsätzen abgekürzt, z. B. mit Milli (m) oder Kilo (k)

Zehnerpotenzen

  • Einheitenvorsätze lassen sich in den meisten Taschenrechnern nicht direkt eingeben
  • Stattdessen wird die Zehnerpotenz verwendet
  • Kilo entspricht 1000 oder $10 \cdot 10 \cdot 10$
  • Abgekürzt $10^3$
$$1500Hz \rArr 1,5kHz \rArr 1,5 \cdot 10^3Hz$$ $$1500000Hz \rArr 1,5MHz \rArr 1,5 \cdot 10^6Hz$$
  • Milli entspricht $\frac{1}{1000}$ oder $\frac{1}{10 \cdot 10 \cdot 10}$
  • Abgekürzt $10^{-3}$
$$0,0035V \rArr 3,5mV \rArr 3,5 \cdot 10^{-3}V$$

Einheitenvorsätze und Zehnerpotenzen

Bezeichnung Abkürzung Wert
Pico p 10-12 = 0,000000000001
Nano n 10-9 = 0,000000001
Mikro µ 10-6 = 0,000001
Milli m 10-3 = 0,001
100 = 1
Kilo k 103 = 1000
Mega M 106 = 1000000
Giga G 109 = 1000000000
Tabelle ES-1.1.1: Einheitenvorsätze für Zehnerpotenzen

Taschenrechner

  • Taste EXP oder ×10x
  • Eintippen: 145,3 ⇒ Exp ⇒ 6
  • Taste ENG verschiebt den Exponent um 3
  • Oft schaltet die Taste S/D zwischen verschiedenen Darstellungen um
EA110: 4200000 Hz entspricht ...

A: $42\cdot 10^{-5}$ Hz.

B: $42\cdot 10^6$ Hz.

C: $4,2\cdot 10^6$ Hz.

D: $4,2\cdot 10^5$ Hz.

EA109: 0,042 A entspricht ...

A: $42\cdot 10^{-3}$ A.

B: $42\cdot 10^3$ A.

C: $42\cdot 10^{-2}$ A.

D: $42\cdot 10^{-1}$ A.

EA108: 0,00042 A entspricht ...

A: $42\cdot 10^{-6}$ A.

B: $420\cdot 10^6$ A.

C: $420\cdot 10^{-6}$ A.

D: $420\cdot 10^{-5}$ A.

EA116: 3750 kHz entspricht ...

A: 0,03750 GHz.

B: 37500000 Hz.

C: 0,3750 GHz.

D: 3,750 MHz.

EA114: $5 \cdot 10^{-1}$ W entspricht ...

A: -500 mW.

B: -5 W.

C: 500 mW.

D: 5 W.

EA111: 0,01 mV entspricht ...

A: $0,01\cdot 10^{3}$ V.

B: $10\cdot 10^{-6}$ V.

C: $1\cdot 10^{-7}$ V.

D: $10\cdot 10^{-5}$ V.

EA112: 0,002 MOhm entspricht ...

A: $20\cdot 10^{3} \Omega$.

B: $2000\cdot 10^{2} \Omega$.

C: $2\cdot 10^{2} \Omega$.

D: $2\cdot 10^{3} \Omega$.

EA115: 0,22 μF entspricht ...

A: 220 nF.

B: 220 pF.

C: 22 nF.

D: 22 pF.

EA113: $2\cdot 10^{-7}$ W entspricht ...

A: 2 μW.

B: 200 μW.

C: 20 μW.

D: 0,2 μW.

Formeln umstellen I

Wir hatten bereits

$$\lambda = \dfrac{c_0}{f}$$

Doch wie kommt man zu

$$c_0 = f \cdot \lambda$$

und

$$f = \dfrac{c_0}{\lambda}$$

?

Mathematischer Ansatz

$\lambda = \dfrac{c_0}{f}$ soll nach $f$ umgestellt werden.

1. Schritt

Multiplikation auf beiden Seiten mit $f$, um es nach links zu bekommen.

$$\lambda = \dfrac{c_0}{f} \quad\quad\quad | \cdot f$$
$$\lambda\cdot f = \dfrac{c_0 \cdot f}{f}$$

Nach Kürzen

$$\lambda \cdot f = c_0$$

2. Schritt

Dividieren auf beiden Seiten mit $\lambda$, um es nach rechts zu bekommen.

$$\lambda \cdot f = c_0 \quad\quad\quad |: \lambda$$
$$\frac{\lambda\cdot f}{\lambda} = \frac{c_0}{\lambda}$$
$$f = \dfrac{c_0}{\lambda}$$

Wellenlänge II

  • Die Wellenlänge $\lambda$ im Freiraum steht zur Frequenz $f$ in Relation mit der Lichtgeschwindigkeit $c_0$
  • Freiraum bedeutet: Vakuum, Luft
  • Lichtgeschwindigkeit $c_0 = 299.792.458 \frac{m}{s}$
  • Im Amateurfunk rechnen wir mit $c = 3\cdot 10^8 \frac{m}{s}$
$$c = f\cdot \lambda \quad f = \dfrac{c}{\lambda} \quad \lambda = \dfrac{c}{f}$$

Vereinfachung

$$f = \dfrac{c}{\lambda} \quad \lambda = \dfrac{c}{f}$$ $$f[[MHz]] \approx \dfrac{300}{\lambda[[m]]} \quad \lambda[[m]] \approx \dfrac{300}{f[[MHz]]}$$
EB314: Welcher Frequenz $f$ entspricht in etwa eine Wellenlänge von 80,0 m im Freiraum?

A: 3,56 MHz

B: 3,75 MHz

C: 3,57 MHz

D: 3,65 MHz

$$f[[MHz]] = \frac{300}{80} = 3,75$$
EB315: Welche Frequenz entspricht in etwa einer Wellenlänge $\lambda$ von 30 mm im Freiraum?

A: 1 GHz

B: 100 MHz

C: 100 GHz

D: 10 GHz

Umrechnen in die Grundeinheit $m$:

$$30mm = 3cm = 0,03m$$ $$f[[MHz]] = \frac{300}{0,03} = \frac{300 \cdot 100}{3} = 10.000$$

$f=10 GHz$, da $1 GHz = 1000 MHz$

EB316: Eine Wellenlänge $\lambda$ von 10 cm im Freiraum entspricht in etwa einer Frequenz von ...

A: 10 GHz.

B: 3 MHz.

C: 3 GHz.

D: 1 GHz.

$$10cm = 0,1m$$ $$f[[MHz]]=\frac{300}{0,1}=3000$$

$3 GHz$, da $1 GHz = 1000 MHz$

EB311: Welcher Wellenlänge $\lambda$ entspricht in etwa die Frequenz 1,84 MHz im Freiraum?

A: 163 m

B: 6,13 m

C: 61,3 m

D: 316 m

EB312: Welcher Wellenlänge $\lambda$ entspricht in etwa die Frequenz $f$ = 21 MHz?

A: 12,86 m

B: 7,15 m

C: 14,29 m

D: 6,43 m

EB313: Welcher Wellenlänge $\lambda$ entspricht in etwa die Frequenz 28,5 MHz im Freiraum?

A: 9,49 cm

B: 10,5 m

C: 15,0 m

D: 9,49 m

Fragen?

Links zu diesem Foliensatz