Reihen- und Parallelschaltung von Bauelementen

Navigationshilfe

Diese Navigationshilfe zeigt die ersten Schritte zur Verwendung der Präsention. Sie kann mit ⟶ (Pfeiltaste rechts) übersprungen werden.

Navigation

Zwischen den Folien und Abschnitten kann man mittels der Pfeiltasten hin- und herspringen, dazu kann man auch die Pfeiltasten am Computer nutzen.

Navigationspfeile für die Präsentation

Weitere Funktionen

Mit ein paar Tastenkürzeln können weitere Funktionen aufgerufen werden. Die wichtigsten sind:

F1
Help / Hilfe
o
Overview / Übersicht aller Folien
s
Speaker View / Referentenansicht
f
Full Screen / Vollbildmodus
b
Break, Black, Pause / Ausblenden der Präsentation
Alt-Click
In die Folie hin- oder herauszoomen

Übersicht

Die Präsentation ist zweidimensional aufgebaut. Dadurch sind in Spalten die einzelnen Abschnitte eines Kapitels und in den Reihen die Folien zu den Abschnitten.

Tippt man ein „o“ ein, bekommt man eine Übersicht über alle Folien des jeweiligen Kapitels. Das hilft sich zunächst einen Überblick zu verschaffen oder sich zu orientieren, wenn man das Gefühlt hat sich „verlaufen“ zu haben. Die Navigation erfolgt über die Pfeiltasten.

Referentenansicht

Referentenansicht

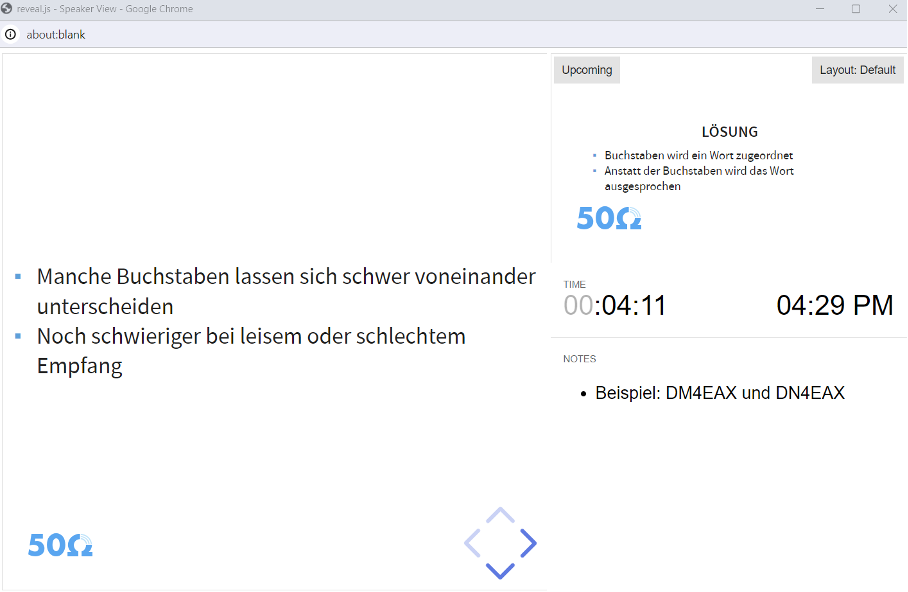
Tippt man ein „s“ ein, bekommt man ein neues Fenster, die Referentenansicht.

Indem man „Layout“ auswählt, kann man zwischen verschieden Anordnungen der Elemente auswählen.

Praxistipps zur Referentenansicht

  • Wenn man mit einem Projektor arbeitet, stellt man im Betriebssystem die Nutzung von 2 Monitoren ein: Die Referentenansicht wird dann zum Beispiel auf dem Laptop angezeigt, während die Teilnehmer die Präsentation angezeigt bekommen.
  • Bei einer Online-Präsentation, wie beispielsweise auf TREFF.darc.de präsentiert man den Browser-Tab und navigiert im „Speaker View“ Fenster.
  • Die Referentenansicht bezieht sich immer auf ein Kapitel. Am Ende des Kapitels muss sie geschlossen werden, um im neuen Kapitel eine neue Referentenansicht zu öffnen.
  • Um mit dem Mauszeiger etwas zu markieren oder den Zoom zu verwenden, muss mit der Maus auf den Bildschirm mit der Präsentation gewechselt werden.

Vollbild

Tippt man ein „f“ ein, wird die aktuelle Folie im Vollbild angezeigt. Mit „Esc“ kann man diesen wieder verlassen.

Das ist insbesondere für den Bildschirm mit der Präsentation für das Publikum praktisch.

Ausblenden

Tippt man ein „b“ ein, wird die Präsentation ausgeblendet.

Sie kann wie folgte wieder eingeblendet werden:

  • Durch klicken in das Fenster.
  • Durch nochmaliges Drücken von „b“.
  • Durch klicken der Schaltfläche „Resume presentation:
Schaltfläche für Resume Presentation

Zoom

Bei gedrückter Alt-Taste und einem Mausklick in der Präsentation wird in diesen Teil hineingezoomt. Das ist praktisch, um Details von Schaltungen hervorzuheben. Durh einen nochmaligen Mausklick zusammen mit Alt wird wieder herausgezoomt.

Das Zoomen funktioniert nur im ausgewählten Fenster. Die Referentenansicht ist hier nicht mit dem Präsenationsansicht gesynct.

Widerstand in Reihen- und Parallelschaltung

Reihenschaltung

Bei einer Reihenschaltung addieren sich die Widerstandswerte

Der folgende Alt-Text wurde noch nicht geprüft: Schaltplan mit drei in Reihe geschalteten Widerständen, beschriftet mit R1, R2 und R3. Links und rechts der Widerstände befinden sich Anschlusspunkte.
Abbildung NEAS-9.1.1: Reihenschaltung von 3 Widerständen

$$R_{ G } = R_{ 1 } + R_{ 2 } + R_{ 3 }$$

Beispiel: $R_{ G } = 100 \Omega + 200 \Omega + 300 \Omega$

Parallelschaltung

Bei einer Parallelschaltung von Widerständen ist der Gesamtwiderstand kleiner als der Wert des kleinsten Widerstandes

Der folgende Alt-Text wurde noch nicht geprüft: Ein elektrischer Schaltplan zeigt drei Widerstände, bezeichnet als R1, R2 und R3. Die Widerstände sind parallel zueinander geschaltet. R1 ist links, R2 in der Mitte und R3 rechts angeordnet. An den Enden der Parallelschaltung befinden sich zwei Knotenpunkte, gekennzeichnet durch schwarze Punkte, die jeweils mit einem offenen Kreis verbunden sind.
Abbildung NEAS-9.1.2: Parallelschaltung von 3 Widerständen

$$\frac{ 1 }{ R_{ G } } = \frac{ 1 }{ R_{ 1 } } + \frac{ 1 }{ R_{ 2 } } + \frac{ 1 }{ R_{ 3 } }$$

Vereinfachung für zwei Widerstände:

$$R_{ G } = \dfrac{ R_{ 1 } \cdot R_{ 2 } }{ R_{ 1 } + R_{ 2 }}$$

Vereinfachung für gleiche Widerstände:

$$R_{ G } = \dfrac{ R }{ n }$$

$n$ steht für die Anzahl der Widerstände

ED104: Zwei Widerstände mit $R_1 = 100 Ohm$ und $R_2 = 400 Ohm$ sind parallel geschaltet. Wie groß ist der Gesamtwiderstand?

A: 300 Ohm

B: 4 Ohm

C: 80 Ohm

D: 500 Ohm

ED105: Zwei Widerstände mit $R_1$ = 50 Ohm und $R_2$ = 200 Ohm sind parallel geschaltet. Wie groß ist der Gesamtwiderstand?

A: 150 Ohm

B: 40 Ohm

C: 250 Ohm

D: 4 Ohm

ED106: Drei gleich große parallel geschaltete Widerstände haben einen Gesamtwiderstand von 1,7 kOhm. Welchen Wert hat jeder Einzelwiderstand?

A: 10 kOhm

B: 2,7 kOhm

C: 560 Ohm

D: 5,1 kOhm

Gemischte Schaltungen

Variante 1: Zwei Parallel und dazu einer in Reihe

Der folgende Alt-Text wurde noch nicht geprüft: Ein Schaltplan mit drei Widerständen, R1, R2 und R3. R1 ist in Reihe mit zwei parallel geschalteten Widerständen R2 und R3. R1 ist links platziert, während R2 oben und R3 unten in der parallelen Anordnung angezeigt werden. Links und rechts vom Schaltbild sind offene Enden.
Abbildung NEAS-9.1.3: Gemischte Schaltung - Variante 1

Hier berechnet man zuerst die Parallelschaltung von $R_2$ und $R_3$ und addiert dann $R_1$ hinzu.

$$R_{ G } = \dfrac{ R_{ 2 } \cdot R_{ 3 } }{ R_{ 2 } + R_{ 3 }} + R_{ 1 }$$

Variante 2: Zwei in Reihe und dazu einer Parallel

Der folgende Alt-Text wurde noch nicht geprüft: Schaltplan mit drei Widerständen, bezeichnet als R1, R2 und R3. R1 und R2 sind in Reihe geschaltet, R3 ist parallel zu diesen beiden. Verbindungen sind mit Linien dargestellt, zwei Anschlusspunkte sind links und rechts außen.
Abbildung NEAS-9.1.4: Gemischte Schaltung - Variante 2

Hier addiert man zuerst $R_1$ und $R_2$ um mit diesem Ergebnis die Parallelschaltung zu $R_3$ zu berechnen.

$$R_{ G } = \dfrac{ (R_{ 1 } + R_{ 2 }) \cdot R_{ 3 }} {( R_{ 1 } + R_{ 2 }) + R_{ 3 }}$$
ED110: Wie groß ist der Gesamtwiderstand der Schaltung? Gegeben: $R_1$ = 500 Ohm, $R_2$ = 1000 Ohm und $R_3$ = 1 kOhm

A: 1 kOhm

B: 5,1 kOhm

C: 2,5 kOhm

D: 501 Ohm

ED111: Wie groß ist der Gesamtwiderstand der Schaltung? Gegeben: $R_1$ = 1 kOhm, $R_2$ = 2000 Ohm und $R_3$ = 2 kOhm

A: 501 Ohm

B: 2 kOhm

C: 5,1 kOhm

D: 2,5 kOhm

ED108: Wie groß ist der Gesamtwiderstand der Schaltung? Gegeben: $R_1$ = 500 Ohm, $R_2$ = 500 Ohm und $R_3$ = 1 kOhm

A: 500 Ohm

B: 2 kOhm

C: 250 Ohm

D: 1 kOhm

ED109: Wie groß ist der Gesamtwiderstand der Schaltung? Gegeben: $R_1$ = 500 Ohm, $R_2$ = 1,5 kOhm und $R_3$ = 2 kOhm

A: 4 kOhm

B: 2 kOhm

C: 1 kOhm

D: 500 Ohm

ED112: Wie groß ist der Gesamtwiderstand dieser Schaltung, wenn $R_1$ = 1 kOhm, $R_2$ = 3 kOhm und $R_3$ = 1500 Ohm betragen?

A: 5,5 kOhm

B: 3,5 kOhm

C: 2 kOhm

D: 1 kOhm

ED113: Wie groß ist der Gesamtwiderstand dieser Schaltung, wenn $R_1$ = 10 kOhm, $R_2$ = 2,5 kOhm, $R_3$ = 500 Ohm und $R_4$ = 600 Ohm betragen?

A: 1 kOhm

B: 13,6 kOhm

C: 7,6 kOhm

D: 200 Ohm

Belastbarkeit von Widerständen in Reihen- und Parallelschaltung

  • Bei einer Reihenschaltung teilen sich die Spannungen auf.
  • Bei einer Parallelschaltung teilen sich die Ströme auf.
  • Somit ist bei der Berechnung mittels $P = U \cdot I$ immer ein Wert konstant und der andere entspechend kleiner.
  • ⇒ die Gesamtbelastbarkeit ist in beiden Fällen größer als die Einzelbelastbarkeit.
ED107: Welche Belastbarkeit kann die Zusammenschaltung von drei gleich großen Widerständen mit einer Einzelbelastbarkeit von je 1 W erreichen, wenn alle 3 Widerstände entweder parallel oder in Reihe geschaltet werden?

A: 1 W bei Parallel- und 3 W bei Reihenschaltung.

B: 1 W bei Parallel- und bei Reihenschaltung.

C: 3 W bei Parallel- und 1 W bei Reihenschaltung.

D: 3 W bei Parallel- und bei Reihenschaltung.

Widerstandsnetzwerke I

  • Bei einer komplexeren Schaltung geht man wie folgt vor: In kleinere Teile auflösen und diese berechnen, danach die Schaltung neu zeichnen und überlegen wie es weitergeht
  • Schauen wir uns die Beispielschaltung mal genauer an
  • $R_5$ und $R_7$ liegen in Reihe und dazu ist $R_8$ parallel geschaltet. Wir berechen diese und nennen den Wert dann $R_{ 5,7,8 }$
  • $R_3$ und $R_6$ liegen in Reihe und dazu ist $R_2$ parallel geschaltet. Wir berechen diese und nennen den Wert dann $R_{ 2,3,6 }$
  • Dann schauen wir uns an, was von der Schaltung übrig geblieben ist.
  • Wir sehen eine Reihenschaltung von 4 Widerständen, die sich leicht berechnen lässt.
  • Damit können wir dann auch die folgenden Prüfungsfragen leicht beantworten.
ED115: Wie groß ist der Gesamtwiderstand der dargestellten Schaltung?

A: 383 Ohm

B: 1150 Ohm

C: 550 Ohm

D: 360 Ohm

ED116: Wie groß ist der Gesamtwiderstand der dargestellten Schaltung?

A: 750 Ohm

B: 950 Ohm

C: 2950 Ohm

D: 120 Ohm

Widerstandsnetzwerke II

Maschen- und Knotenregel

Maschenregel: In jedem geschlossenen Stromkreis (Masche) ist die Summe der Spannungen gleich null. Knotenregel: In jedem Knotenpunkt ist die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme.

AD106: Wie groß ist die Spannung $U$, wenn durch $R_3$ ein Strom von 1 mA fließt und alle Widerstände $R_1$ bis $R_3$ je 10 kOhm betragen?

A: 40 V

B: 20 V

C: 15 V

D: 30 V

Lösungsweg

  • gegeben: $R_1 = R_2 = R_3 = 10kΩ$
  • gegeben: $I_3 = I_2 = 1 mA$
  • gesucht: $U$
$$R_{ges} = R_1 + \frac{R_1 \cdot R_2}{R_1 + R_2} = 10kΩ + \frac{10kΩ \cdot 10kΩ}{10kΩ + 10kΩ} = 15kΩ$$
$$I_{ges} = I_2 + I_3 = 1mA + 1mA = 2mA$$
$$U = R_{ges} \cdot I_{ges} = 15kΩ \cdot 2mA = 30V$$
AD107: Wie groß ist der Strom durch $R_3$, wenn $U$ = 15 V und alle Widerstände $R_1$ bis $R_3$ je 10 kOhm betragen?

A: 0,5 mA

B: 1,6 mA

C: 4,5 mA

D: 1,0 mA

Lösungsweg

  • gegeben: $R_1 = R_2 = R_3 = 10kΩ$
  • gegeben: $U=15 V$
  • gesucht: $I_3$
$$R_{ges} = R_1 + \frac{R_1 \cdot R_2}{R_1 + R_2} = 10kΩ + \frac{10kΩ \cdot 10kΩ}{10kΩ + 10kΩ} = 15kΩ$$
$$\frac{U_3}{U} = \frac{R_{2\parallel 3}}{R_{ges}} \Rightarrow U_3 = \frac{R_{2\parallel 3}}{R_{ges}} \cdot U = \frac{5kΩ}{15kΩ} \cdot 15V = 5V$$
$$I_3 = \frac{U_3}{R_3} = \frac{5V}{10kΩ} = 0,5mA$$
AD108: Welche Leistung tritt in $R_2$ auf, wenn $U$ = 15 V und alle Widerstände $R_1$ bis $R_3$ je 10 kOhm betragen?

A: 1,5 mW

B: 0,15 W

C: 2,5 mW

D: 5,0 mW

Lösungsweg

  • gegeben: $R_1 = R_2 = R_3 = 10kΩ$
  • gegeben: $U=15 V$
  • gesucht: $P_2$
$$\frac{U_2}{U} = \frac{R_{2\parallel 3}}{R_{ges}} \Rightarrow U_2 = \frac{R_{2\parallel 3}}{R_{ges}} \cdot U = \frac{5kΩ}{15kΩ} \cdot 15V = 5V$$
$$P_2 = \frac{U_2^2}{R_2} = \frac{(5V)^2}{10kΩ} = 2,5mW$$
AD109: In welchem Bereich liegt der Eingangswiderstand der folgenden Schaltung, wenn $R$ alle Werte von 0 Ohm bis 1 kOhm annehmen kann?

A: 300 bis 367 Ohm

B: 292 bis 367 Ohm

C: 267 bis 292 Ohm

D: 300 bis 500 Ohm

Lösungsweg

  • gegeben: $R = 0\dots 1kΩ$
  • gegeben: $R_1 = 200Ω$
$$R_{ges} = R_1 + \frac{R_2 \cdot (R_3 + R)}{R_2 + (R_3 + R)}$$

Bei $R = 0Ω$:

$$R_{ges} = 200Ω + \frac{100Ω \cdot (200Ω + 0Ω)}{100Ω + 200Ω +0Ω} \approx 267Ω$$

Bei $R = 1kΩ$:

$$R_{ges} = 200Ω + \frac{100Ω \cdot (200Ω + 1kΩ)}{100Ω + 200Ω +1kΩ} \approx 292Ω$$
AD110: Wenn $\textrm{R}_1$ und $\textrm{R}_3$ je 2,2 kOhm haben und $\textrm{R}_2$ und $\textrm{R}_4$ je 220 Ohm betragen, hat die Schaltung zwischen den Punkten a und b einen Gesamtwiderstand von ...

A: 1540 Ohm.

B: 4840 Ohm.

C: 2420 Ohm.

D: 1210 Ohm.

Lösungsweg

  • gegeben: $R_1 = R_3 = 2,2kΩ$
  • gegeben: $R_2 = R_4 = 220Ω$
  • gesucht: $R_{ges}$
$$\begin{equation}\begin{split}\nonumber R_{ges} &= \frac{(R_1 + R_2) \cdot (R_3 + R_4)}{(R_1 + R_2) + (R_3 + R_4)}\\ &= \frac{(2,2kΩ + 220Ω) \cdot (2,2kΩ + 220Ω)}{2,2kΩ + 220Ω + 2,2kΩ + 220Ω}\\ &= 1210Ω\end{split}\end{equation}$$
AD114: Wie groß ist die Spannung $U_2$ in der Schaltung mit folgenden Werten: $U_{\textrm{B}} = 12 V$, $R_1 = 10 k\Omega$, $R_2 = 2,2 k\Omega$, $R_{\textrm{L}} = 8,2 k\Omega$

A: 8,2 V

B: 5,4 V

C: 1,8 V

D: 2,2 V

Lösungsweg

  • gegeben: $R_1 = 10kΩ$
  • gegeben: $R_2 = 2,2kΩ$
  • gegeben: $R_L = 8,2kΩ$
$$\frac{U_2}{U_B} = \frac{R_{2\parallel L}}{R_{ges}}$$ $$R_{2\parallel L} = \frac{R_2 \cdot R_L}{R_2 + R_L} = \frac{2,2kΩ \cdot 8,2kΩ}{2,2kΩ + 8,2kΩ} = 1,74kΩ$$ $$R_{ges} = R_1 + R_{2\parallel L} = 10kΩ + 1,74kΩ = 11,74kΩ$$
$$U_2 = \frac{R_{2\parallel L}}{R_{ges}} \cdot U_B = \frac{1,74kΩ}{11,74kΩ} \cdot 12V \approx 1,8V$$

Spannungsteiler I

  • Eine Reihenschaltung von Widerständen nennt man auch Spannungsteiler, weil die Spannungen sich an den Widerständen aufteilen.
  • Je größer der Widerstand, desto größer die Spannung, die an ihm abfällt.
  • Das kann man mathematisch in folgender Formel ausdrücken (Formelsammlung):
$$\dfrac{ U_{ 1 } }{ U_{ 2 } } = \dfrac{ R_{ 1 } }{ R_{ 2 } }$$

Wie geht man an die Aufgaben ran?

  • Beispiele:
  • Wenn $R_{ 1 }$ drei mal so groß wie $R_{ 2 }$ ist, ist $U_{ 1 }$ drei mal so groß wie $U_{ 2 }$.
  • Wenn $R_{ 1 }$ $\frac{ 1 }{ 3 }$ so groß wie $R_{ 2 }$ ist, ist $U_{ 1 }$ $\frac{ 1 }{ 3 }$ so groß wie $U_{ 2 }$.

Schauen wir uns dazu zwei Aufgaben an.

ED101: Wie teilt sich die Spannung an zwei in Reihe geschalteten Widerständen auf, wenn $R_1$ = 5-mal so groß ist wie $R_2$?

A: $U_1 = \frac{U_2}{5}$

B: $U_1 = \frac{U_2}{6}$

C: $U_1 = 5\cdot U_2$

D: $U_1 = 6\cdot U_2$

ED102: Wie teilt sich die Spannung an zwei in Reihe geschalteten Widerständen auf, wenn $R_1 = \frac{1}{6}$ von $R_2$ ist?

A: $U_1 = \frac{U_2}{6}$

B: $U_1 = 5\cdot U_2$

C: $U_1 = \frac{U_2}{5}$

D: $U_1 = 6\cdot U_2$

  • Die Summe der Spannnungsabfälle ist gleich der Spannung, die aus der Spannungsquelle herauskommt.
  • Das kann man mathematisch in folgender Formel ausdrücken (Formelsammlung):
$$U_{ G } = U_{ 1 } + U_{ 2 }$$
  • Hat man eine Gesamtspannung und muss $U_{ 2 }$ berechnen, können wir ebenfalls auf eine Formel aus der Formelsammlung zurückgreifen:
$$\dfrac{ U_{ 2 } }{ U_{ G } } = \dfrac{ R_{ 2 } }{ R_{ 1 } + R_{ 2 } }$$
  • Diese muss man noch zu $U_{ 2 }$ umstellen, indem man auf beiden Seiten mit $U_{ G }$ multipliziert, dann erhält man:
$$U_{ 2 } = \dfrac{ R_{ 2 } }{ R_{ 1 } + R_{ 2 } } \cdot U_{ G }$$
  • Damit kann man sich dann auch an die nächste Aufgabe heranwagen.
ED103: Die Gesamtspannung $U$ an folgendem Spannungsteiler beträgt 9 V. Die Widerstände haben die Werte $R_1$ = 10 kOhm und $R_2$ = 20 kOhm. Wie groß ist die Teilspannung $U_2$?

A: 3,0 V

B: 6,0 V

C: 4,5 V

D: 7,5 V

Spannungsteiler II

Belasteter Spannungsteiler

  • Gesamtstrom steigt, wenn die Belastung erhöht wird, also wenn $R_{\textrm{L}}$ niederohmiger wird
  • Voraussetzung: Strom der Versorgung bricht nicht ein
  • Bei der Dimensionierung auf die Stromstärken durch die Widerstände achten
AD115: Wenn der dargestellte Spannungsteiler mit $R_{\textrm{L}}$ belastet wird, dann ergibt sich folgender Zusammenhang:

A: $I_2$ steigt, $R_1$ setzt weniger Leistung in Wärme um.

B: $I_1$ sinkt, $R_2$ setzt mehr Leistung in Wärme um.

C: $I_1$ steigt, $R_1$ setzt mehr Leistung in Wärme um.

D: $I_1$ steigt, $R_2$ setzt mehr Leistung in Wärme um.

Lösungsweg

Im belasteten Spannungsteiler fließen 3 Ströme:

  • $I_1$ fließt durch $R_1$ und verursacht dort eine Verlustleistung $P_1 = U_1 \cdot I_1 = I_2 \cdot R_1$
  • $I_2$ fließt durch $R_2$ und verursacht dort eine Verlustleistung $P_2 = U_2 \cdot I_2 = {I_2}^2 \cdot R_2$
  • $I_L$ fließt durch $R_L$ und verursacht dort eine Verlustleistung $P_L = U_2 \cdot I_L = {I_L}^2 \cdot R_L$
  • Der Strom $I_1$ ist die Summe von $I_2$ und $I_L$ und damit der größte Strom.

Brückenschaltung

Der folgende Alt-Text wurde noch nicht geprüft: Ein Schaltplan zeigt vier Widerstände, die mit R1, R2, R3 und R4 beschriftet sind. Diese sind in einem rechteckigen Muster angeordnet. Eine Quelle, gekennzeichnet mit einem
Abbildung NEAS-9.6.1: Typische Brückenschaltung mit 4 Widerständen

$$\frac{R_1}{R_2} = \frac{R_3}{R_4}$$
AD111: In welchem Verhältnis müssen die Widerstände $R_1$ bis $R_4$ zueinander stehen, damit das Messinstrument im Brückenzweig keine Spannung anzeigt?

A: $\dfrac{R_2}{R_1} = \dfrac{R_3}{R_4}$

B: $\dfrac{R_1}{R_4} = \dfrac{R_2}{R_3}$

C: $\dfrac{R_1}{R_2} = \dfrac{R_3}{R_4}$

D: $\dfrac{R_1}{R_2} = \dfrac{R_4}{R_3}$

AD112: Die Spannung an der Brückenschaltung beträgt 10 V. Alle Widerstände haben einen Wert von 50 Ohm. Wie groß ist die Spannung zwischen A und B im Brückenzweig (gemessen von A nach B)?

A: 0 V

B: -5 V

C: 2,5 V

D: 5 V

AD113: Die Spannung an der Brückenschaltung beträgt 11 V. Die Widerstände haben folgende Werte: $R_1$ = 1 kOhm; $R_2$ = 10 kOhm; $R_3$ = 10 kOhm; $R_4$ = 1 kOhm. Wie groß ist die Spannung zwischen A und B im Brückenzweig (gemessen von A nach B)?

A: $U_{AB} = 9 V$

B: $U_{AB} = -10 V$

C: $U_{AB} = -9 V$

D: $U_{AB} = 10 V$

Lösungsweg

  • gegeben: $R_1 = R_4 = 1kΩ$
  • gegeben: $R_2 = R_3 = 10kΩ$
  • gegeben: $U = 11 V$
  • gesucht: $U_{AB}$
$$\frac{U_A}{U} = \frac{R_1}{R_1 + R_2} \Rightarrow U_A = \frac{R_1}{R_1 + R_2} \cdot U = \frac{1kΩ}{1kΩ + 10kΩ} \cdot 11V = 1V$$
$$\frac{U_B}{U} = \frac{R_3}{R_3 + R_4} \Rightarrow U_B = \frac{R_3}{R_3 + R_4} \cdot U = \frac{10kΩ}{10kΩ + 1kΩ} \cdot 11V = 10V$$
$$U_{AB} = |U_A - U_B| = |1V - 10V| = 9V$$

Kondensator in Reihen- und Parallelschaltung

Reihenschaltung

  • Da die Spannung entscheidend für das Entstehen des elektrischen Feldes ist (und diese sich bei der Reihenschaltung aufteilt), ist die Berechung der Kapazität genau umgekehrt wie bei Widerständen.
  • Anwendungsfall: Bei hohen Spannungen werden mehrere Kondensatoren in Reihe geschaltet, um die Gefahr eines Durchschlags zu verhindern. Dabei ist hilfreich, dass sich die Gesamtspannung an den Kondensatoren aufteilt.
  • Bei einer Reihenschaltung von Kondensatoren ist die Gesamtkapazität kleiner als der Wert des kleinsten Kondensators

Der folgende Alt-Text wurde noch nicht geprüft: 1) Kurze Zusammenfassung: Ein Schaltplan zeigt drei in Reihe geschaltete Kondensatoren zwischen zwei runden Anschlussknoten. 2) Detaillierte Beschreibung: Auf einer waagerechten Leitung befindet sich links ein kleiner offener Kreis als Anschlusspunkt; die Leitung führt nach rechts zum ersten Kondensatorsymbol C1 (zwei senkrechte, parallele Platten mit kleinem Zwischenraum), darüber steht die Beschriftung „C1“. Von dort verläuft die Leitung weiter nach rechts zum zweiten, identisch gezeichneten Kondensator mit der Beschriftung „C2“ oberhalb, anschließend weiter zum dritten gleichartigen Kondensator mit der Beschriftung „C3“ oberhalb. Rechts endet die Leitung in einem zweiten kleinen offenen Kreis als Anschlusspunkt. Weitere Bauteile, Skalen oder Beschriftungen sind nicht vorhanden.
Abbildung NEAS-9.7.1: Reihenschaltung von 3 Kondensatoren

$$\frac{ 1 }{ C_{ G } } = \frac{ 1 }{ C_{ 1 } } + \frac{ 1 }{ C_{ 2 } } + \frac{ 1 }{ C_{ 3 } }$$
  • Vereinfachung für zwei Kondensatoren:
$$C_{ G } = \dfrac{ C_{ 1 } \cdot C_{ 2 } }{ C_{ 1 } + C_{ 2 }}$$
  • Vereinfachung für gleiche Kondensatoren:
$$C_{ G } = \dfrac{ C }{ n }$$

$n$ steht für die Anzahl der Kondensatoren

ED119: Eine Reihenschaltung besteht aus drei Kondensatoren von je 0,33 μF. Wie groß ist die Gesamtkapazität dieser Schaltung?

A: 0,099 μF

B: 0,011 μF

C: 0,990 μF

D: 0,110 μF

ED120: Welche Gesamtkapazität ergibt sich bei einer Reihenschaltung der Kondensatoren 100 μF, 200000 nF und 200 μF?

A: 50 μF

B: 102 μF

C: 320 nF

D: 300,2 μF

Parallelschaltung

  • Hier ist es genau umgekehrt wie bei Widerständen, weil an allen Kondensatoren die gleiche Spannung anliegt, welche ja entscheidend für die Entstehung des elektrischen Feldes ist.
  • Anwendungsfall: Kondensatoren werden parallel geschaltet, um aus der Normreihe auf den Wert zu kommen, den man benötigt.
  • Bei einer Parallelschaltung addieren sich die Kapazitäten

Der folgende Alt-Text wurde noch nicht geprüft: Zusammenfassung: Schaltplan mit drei Kondensatoren C1, C2 und C3 in einem rechteckigen Leitungsrahmen und einem mittigen vertikalen Leiter mit zwei Anschlussklemmen oben und unten. Detaillierte Beschreibung: Ein rechteckiger Drahtrahmen bildet den äußeren Stromweg mit einer oberen und einer unteren Horizontalleitung sowie linken und rechten Vertikalzweigen. Im linken Vertikalzweig ist ein Kondensator mit zwei parallelen Platten eingezeichnet, daneben die Beschriftung „C1“. Im rechten Vertikalzweig ist ein gleiches Kondensatorsymbol mit der Beschriftung „C3“ zu sehen. In der Mitte verläuft ein senkrechter Leiter, der die obere und untere Horizontalleitung verbindet; an den beiden Kreuzungspunkten sind ausgefüllte Knotenpunkte (schwarze Punkte) markiert. Zwischen diesen beiden Knoten liegt in der Mitte des senkrechten Leiters ein weiterer Kondensator, ebenfalls als zwei parallele Platten gezeichnet, mit der Beschriftung „C2“. Der mittlere Leiter setzt sich über die obere Kante nach oben und über die untere Kante nach unten fort und endet jeweils in einer kleinen offenen Anschlussmarkierung (ein Kreis). Es sind keine Werte, Polaritätszeichen oder weiteren Texte vorhanden.
Abbildung NEAS-9.7.2: Parallelschaltung von 3 Kondensatoren

$$C_{ G } = C_{ 1 } + C_{ 2 } + C_{ 3 }$$
ED117: Drei Kondensatoren mit den Kapazitäten $C_1$ = 0,1 μF, $C_2$ = 150 nF und $C_3$ = 50000 pF werden parallel geschaltet. Wie groß ist die Gesamtkapazität?

A: 0,3 μF

B: 0,255 μF

C: 0,027 μF

D: 0,2 μF

ED118: Wie groß ist die Gesamtkapazität von drei parallel geschalteten Kondensatoren von 22 nF, 0,033 μF und 15000 pF?

A: 40,3 nF

B: 0,070 μF

C: 700 nF

D: 7021 pF

Gemischte Schaltungen

Variante 1: Zwei Parallel und dazu einer in Reihe

  • Hier berechnet man zuerst die Parallelschaltung von $C_{ 2 }$ und $C_{ 3 }$
$$C_{ Gp } = C_{ 2 } + C_{ 3 }$$
  • Danach berechnet man die Reihenschaltung von $C_{ 1 }$ und $C_{ Gp }$
$$C_{ G } = \frac{ C_{ 1 } \cdot C_{ Gp } }{ C_{ 1 } + C_{ Gp }}$$
ED123: Welche Gesamtkapazität hat die folgende Schaltung? Gegeben: $C_1$ = 8 nF; $C_2$ = 4 nF; $C_3$ = 4 nF

A: 4 nF

B: 16 nF

C: 1 nF

D: 9 nF

ED124: Welche Gesamtkapazität hat diese Schaltung, wenn $C_1$ = 200 nF, $C_2$ = 100 nF und $C_3$ = 100000 pF betragen?

A: 250 nF

B: 400 nF

C: 200 nF

D: 100 nF

ED122: Welche Gesamtkapazität hat diese Schaltung, wenn $C_1$ = 2 μF, $C_2$ = 1 μF und $C_3$ = 1 μF betragen?

A: 1,0 μF

B: 4,0 μF

C: 2,5 μF

D: 4400 nF

Variante 2: Zwei in Reihe und dazu einer Parallel

  • Hier berechnet man zuerst die Reihenschaltung von $C_{ 1 }$ und $C_{ 2 }$
$$C_{ Gr } = \frac{ C_{ 1 } \cdot C_{ 2 } }{ C_{ 1 } + C_{ 2 }}$$
  • Danach berechnet man die Parallelschaltung von $C_{ 3 }$ und $C_{ Gr }$
$$C_{ G } = \frac{ C_{ 3 } \cdot C_{ Gr } }{ C_{ 3 } + C_{ Gr }}$$
ED121: Welche Gesamtkapazität hat die folgende Schaltung? Gegeben: $C_1$ = 10 nF; $C_2$ = 10 nF; $C_3$ = 5 nF

A: 20 nF

B: 10 nF

C: 5 nF

D: 25 nF

Spule in Reihenschaltung

Der folgende Alt-Text wurde noch nicht geprüft: Zusammenfassung: Nahaufnahme des Innenraums eines elektronischen Geräts mit einer dicht gewickelten roten Zylinderspule und zahlreichen Drahtabgriffen, die zu einem mehrstufigen Drehschalter im Metallchassis führen. Detaillierte Beschreibung: Im unteren Bildbereich liegt horizontal eine rote, zylindrische Spule, eng mit dunkelrotem Kupferdraht bewickelt. Entlang der oberen Spulenseite sind viele Abgriffe sichtbar: dünne, bräunliche lackierte Drähte, die an einzelnen Windungen angelötet sind; an den Lötstellen sitzen silbrig glänzende Lottropfen, teils mit dunklen Verfärbungen an der Umgebung. Die Abgriffe verlaufen bogenförmig nach oben und vorne zu einem gestapelten, kreisförmigen Drehschalter mit mehreren Isolatorscheiben und radial angeordneten Lötfahnen. In der Schaltermitte sitzt eine Metallwelle mit Federn und kleinen mechanischen Teilen. Links und rechts erkennt man das graue Metallchassis mit Schrauben, Federn und Halterungen; einzelne weiße und graue Leitungen führen in den Aufbau. Der Hintergrund ist überwiegend grau-metallisch, unter der Spule ist ein heller, weißer Untergrund zu sehen. Der Gesamteindruck ist technisch, gebraucht und funktional, mit leicht unordentlich geführten Drähten.
Abbildung NEAS-9.8.1: Spule mit 14 Anzapfungen in einem selbstgebauten Antennenanpassgerät

$$L_\text{G} = L_1 + L_2 + L_3 + ... + L_n$$
AD102: Wie groß ist die Gesamtinduktivität von drei in Reihe geschalteten Spulen von 2200 nH, 0,033 mH und 150 μH?

A: 185,2 μH

B: 155,5 μH

C: 205,0 nH

D: 205,0 μH

Lösungsweg

$$L_{ges} = 2200nH + 0,033mH + 150µH = 185,2µH$$

Reihen- und Parallelschaltung gemischter Bauelemente

Parallelschwingkreis

  • Spulen und Kondensatoren werden kombiniert
  • Zu beachten ist auch die Wicklungskapazität
  • Dadurch kommen „unsichtbare“ Kapazitäten mit in die Schaltung
AD101: Wie groß ist die Gesamtkapazität, wenn drei Kondensatoren $C_1$ = 0,10 nF, $C_2$ = 47 pF und $C_3$ = 22 pF in Reihe geschaltet werden?

A: 16,9 pF

B: 0,13 nF

C: 13,0 pF

D: 169 pF

Lösungsweg

  • gegeben: $C_1 = 0,10 nF$
  • gegeben: $C_2 = 47 pF$
  • gegeben: $C_3 = 22 pF$
  • gesucht: $C_{\textrm{ges}}$
$$\begin{equation}\begin{align}\nonumber \tfrac{1}{C_{\textrm{ges}}} &= \tfrac{1}{C_1} + \tfrac{1}{C_2} + \tfrac{1}{C_3} = \tfrac{1}{0,10nF} + \tfrac{1}{47pF} + \tfrac{1}{22pF}\\ \nonumber &= 7,67\cdot 10^{10} \tfrac{1}{F}\\ \nonumber \Rightarrow C_{\textrm{ges}} &= \frac{1}{7,67\cdot 10^{10} \frac{1}{F}} \approx 13,0pF \end{align}\end{equation}$$
AD103: Wie groß ist die Gesamtkapazität dieser Schaltung, wenn $C_1$ = 0,1 nF, $C_2$ = 1,5 nF, $C_3$ = 220 pF und die Eigenkapazität der Spule 1 pF beträgt?

A: 1821 pF

B: 1 pF

C: 1,6 nF

D: 66 pF

Lösungsweg

  • gegeben: $C_1 = 0,1 nF$
  • gegeben: $C_2 = 1,5 nF$
  • gegeben: $C_3 = 220 pF$
  • gegeben: $C_{\textrm{L}} = 1 pF$
  • gesucht: $C_{\textrm{ges}}$
$$\begin{equation}\begin{split}\nonumber C_{\textrm{ges}} &= C_1 + C_2 + C_3 + C_{\textrm{L}}\\ &= 0,1nF + 1,5nF + 220pF + 1pF\\ &= 1821pF \end{split}\end{equation}$$
AD105: Berechne den Betrag des Scheinwiderstands $Z$ für eine Reihenschaltung aus $R$ = 100 Ohm und $L$ = 100 μH bei 1 MHz.

A: $|Z|$ = 259 Ohm

B: $|Z|$ = 628 Ohm

C: $|Z|$ = 636 Ohm

D: $|Z|$ = 188 Ohm

Lösungsweg

  • gegeben: $R = 100\Omega$
  • gegeben: $L = 100\mu H$
  • gegeben: $f = 1 MHz$
  • gesucht: $Z$
$$\begin{equation}\begin{split}\nonumber X_{\textrm{L}} &= \omega \cdot L = 2 \cdot \pi \cdot f \cdot L\\ &= 2 \cdot \pi \cdot 1MHz \cdot 100\mu H = 628\Omega\end{split}\end{equation}$$
$$Z = \sqrt{R^2 + X^2} = \sqrt{(100\Omega)^2 + (628\Omega)^2} \approx 636\Omega$$
AD104: Berechne den Betrag des Scheinwiderstands $Z$ für eine Reihenschaltung aus $R$ = 100 Ohm und $C$ = 1 nF bei 1 MHz.

A: $|Z|$ = 188 Ohm

B: $|Z|$ = 159 Ohm

C: $|Z|$ = 259 Ohm

D: $|Z|$ = 636 Ohm

Lösungsweg

  • gegeben: $R = 100\Omega$
  • gegeben: $C = 100 nF$
  • gegeben: $f = 1 MHz$
  • gesucht: $Z$
$$\begin{equation}\begin{split}\nonumber X_{\textrm{C}} &= \frac{1}{\omega \cdot C} = \frac{1}{2 \cdot \pi \cdot f \cdot C}\\ &= \frac{1}{2 \cdot \pi \cdot 1MHz \cdot 100nF} = 159\Omega\end{split}\end{equation}$$
$$Z = \sqrt{R^2 + X^2} = \sqrt{(100\Omega)^2 + (159\Omega)^2} \approx 188\Omega$$

Fragen?

Links zu diesem Foliensatz