Bauelemente

Navigationshilfe

Diese Navigationshilfe zeigt die ersten Schritte zur Verwendung der Präsention. Sie kann mit ⟶ (Pfeiltaste rechts) übersprungen werden.

Navigation

Zwischen den Folien und Abschnitten kann man mittels der Pfeiltasten hin- und herspringen, dazu kann man auch die Pfeiltasten am Computer nutzen.

Navigationspfeile für die Präsentation

Weitere Funktionen

Mit ein paar Tastenkürzeln können weitere Funktionen aufgerufen werden. Die wichtigsten sind:

F1
Help / Hilfe
o
Overview / Übersicht aller Folien
s
Speaker View / Referentenansicht
f
Full Screen / Vollbildmodus
b
Break, Black, Pause / Ausblenden der Präsentation
Alt-Click
In die Folie hin- oder herauszoomen

Übersicht

Die Präsentation ist zweidimensional aufgebaut. Dadurch sind in Spalten die einzelnen Abschnitte eines Kapitels und in den Reihen die Folien zu den Abschnitten.

Tippt man ein „o“ ein, bekommt man eine Übersicht über alle Folien des jeweiligen Kapitels. Das hilft sich zunächst einen Überblick zu verschaffen oder sich zu orientieren, wenn man das Gefühlt hat sich „verlaufen“ zu haben. Die Navigation erfolgt über die Pfeiltasten.

Referentenansicht

Referentenansicht

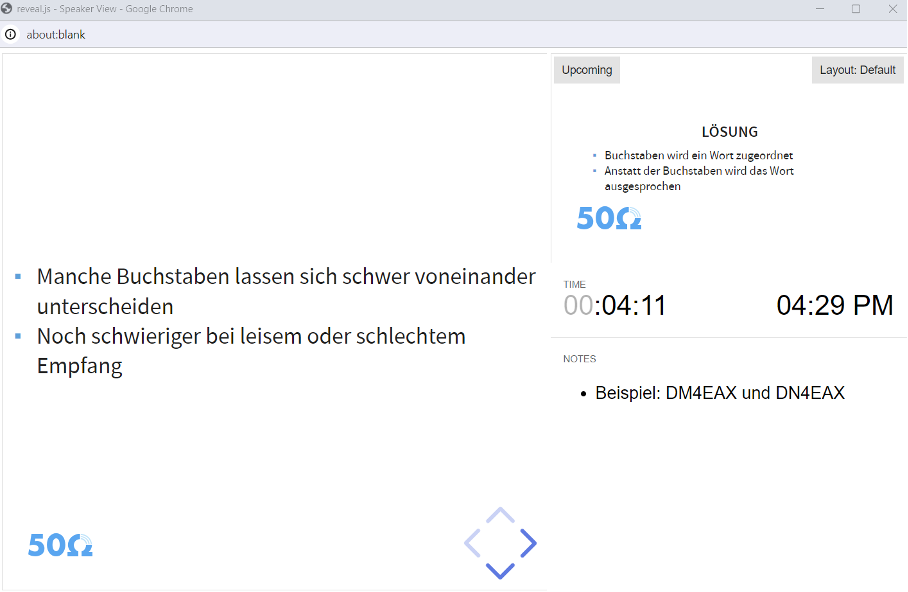
Tippt man ein „s“ ein, bekommt man ein neues Fenster, die Referentenansicht.

Indem man „Layout“ auswählt, kann man zwischen verschieden Anordnungen der Elemente auswählen.

Praxistipps zur Referentenansicht

  • Wenn man mit einem Projektor arbeitet, stellt man im Betriebssystem die Nutzung von 2 Monitoren ein: Die Referentenansicht wird dann zum Beispiel auf dem Laptop angezeigt, während die Teilnehmer die Präsentation angezeigt bekommen.
  • Bei einer Online-Präsentation, wie beispielsweise auf TREFF.darc.de präsentiert man den Browser-Tab und navigiert im „Speaker View“ Fenster.
  • Die Referentenansicht bezieht sich immer auf ein Kapitel. Am Ende des Kapitels muss sie geschlossen werden, um im neuen Kapitel eine neue Referentenansicht zu öffnen.
  • Um mit dem Mauszeiger etwas zu markieren oder den Zoom zu verwenden, muss mit der Maus auf den Bildschirm mit der Präsentation gewechselt werden.

Vollbild

Tippt man ein „f“ ein, wird die aktuelle Folie im Vollbild angezeigt. Mit „Esc“ kann man diesen wieder verlassen.

Das ist insbesondere für den Bildschirm mit der Präsentation für das Publikum praktisch.

Ausblenden

Tippt man ein „b“ ein, wird die Präsentation ausgeblendet.

Sie kann wie folgte wieder eingeblendet werden:

  • Durch klicken in das Fenster.
  • Durch nochmaliges Drücken von „b“.
  • Durch klicken der Schaltfläche „Resume presentation:
Schaltfläche für Resume Presentation

Zoom

Bei gedrückter Alt-Taste und einem Mausklick in der Präsentation wird in diesen Teil hineingezoomt. Das ist praktisch, um Details von Schaltungen hervorzuheben. Durh einen nochmaligen Mausklick zusammen mit Alt wird wieder herausgezoomt.

Das Zoomen funktioniert nur im ausgewählten Fenster. Die Referentenansicht ist hier nicht mit dem Präsenationsansicht gesynct.

Phase

Sinusförmige Wechselspannung

Der folgende Alt-Text wurde noch nicht geprüft: Zusammenfassung: Die Grafik zeigt links einen Kreis mit mehreren farbigen Pfeilen und rechts eine graue Sinuskurve U(t) mit Zeitachse sowie darunter Skalen für Drehwinkel φ in Grad und im Bogenmaß. Details: Links ist ein dünn gezeichneter grauer Kreis mit einem schwarzen Mittelpunkt. Vom Mittelpunkt gehen farbige Pfeile aus: ein gelber Pfeil „A“ zeigt schräg nach oben rechts, ein grüner Pfeil „B“ zeigt nach oben, ein cyanfarbener Pfeil „D“ nach unten, und ein orangefarbener Pfeil „C“ nach links; die Buchstaben „A“, „B“, „C“, „D“ stehen farblich passend neben den Pfeilspitzen. Von der oberen und unteren Kreisposition führen dort ansetzende, punktierte horizontale Linien (grün oben, cyan unten) nach rechts; eine orange punktierte Linie verläuft mittig horizontal nach rechts. Rechts daneben beginnt ein Koordinatensystem mit senkrechter Achse „U“ (Pfeil nach oben) bei t = 0 und einer waagerechten Zeitachse „t“ (beschriftet „Zeit“, Pfeil nach rechts). Auf der Zeitachse sind Markierungen mit Beschriftungen 0, T/4, T/2, 3T/4, T, 5T/4. Eine graue Sinuskurve startet bei t = 0 bei U = 0, steigt zum positiven Maximum nahe T/4, fällt durch 0 bei T/2 zum negativen Minimum nahe 3T/4 und kehrt bei T wieder zu 0 zurück; rechts deutet ein Pfeil die Fortsetzung an. Unter der Zeitachse sind zwei weitere waagerechte Skalen mit Pfeilen nach rechts: „Drehwinkel φ“ mit Teilungen und Beschriftungen 0°, 90°, 180°, 270°, 360°, 450°, sowie darunter „Bogenmaß φ“ mit 0, π/2, π, 3π/2, 2π, 5π/2.
Abbildung AS-3.1.1: Phasenwinkel in Grad und Bogenmaß oder Periodendauerangabe

AB302: Welche Antwort enthält die richtigen Phasenwinkel der dargestellten sinusförmigen Wechselspannung an der mit X$_3$ bezeichneten Stelle?

A: $\dfrac{3\pi}{4}; 135 °$

B: $\dfrac{3\pi}{2}; 270 °$

C: $\dfrac{\pi}{3}; 270 °$

D: $3\pi; 180 °$

Phasenverschiebung

  • Schaltungen mit Kondensatoren, Spulen und Widerständen
  • Phasenverschiebung zwischen anliegender sinusförmiger Wechselspannung und fließendem sinusförmigen Wechselstrom
AB303: Der Betrag der Phasendifferenz zwischen den beiden in der Abbildung dargestellten Sinussignalen ist ...

A: 180 °.

B: 0 °.

C: 90 °.

D: 45 °.

Kondensator II

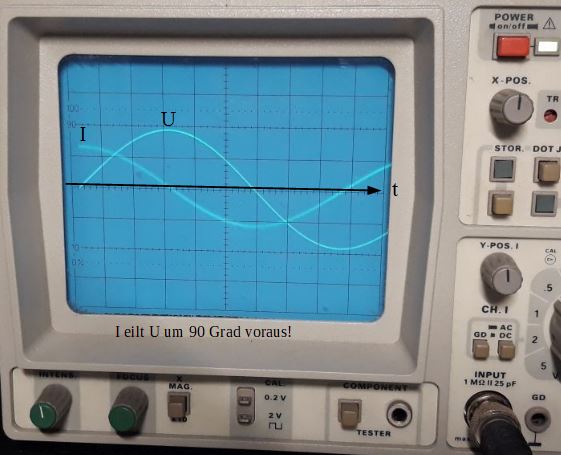
Der folgende Alt-Text wurde noch nicht geprüft: 1. Zusammenfassung: Ein analoges Oszilloskop zeigt zwei phasenverschobene Sinuskurven auf blauem Raster, daneben sind zahlreiche Drehknöpfe und Tasten der Frontplatte sichtbar. 2. Details: Das Gerät ist frontal zu sehen, links der rechteckige CRT-Bildschirm mit feinem, hellblauem Gitter. Auf dem Schirm verlaufen zwei hellblaue Sinuskurven; die obere ist mit „I“ beschriftet und liegt zeitlich vor der unteren, die mit „U“ markiert ist. Eine horizontale Referenzlinie mit Pfeil nach rechts ist mit „t“ gekennzeichnet. Am unteren Bildschirmrand steht der Text „I eilt U um 90 Grad voraus!“. Rechts vom Bildschirm befindet sich die Bedieneinheit mit einem Schalter „POWER on/off“, Drehknöpfen „X-POS.“ und „Y-POS. I“, Tastenfeldern und einem Bereich „CH. I“. Unten rechts ist eine Eingangsbuchse mit der Beschriftung „INPUT 1 MΩ 25 pF“ zu sehen, unten links mehrere Regler wie „INTEN“, „FOCUS“, „MAG.“, „CAL 0.2V“ sowie ein Feld „COMPONENT TESTER“. Das Gehäuse ist hellgrau, die Bedienelemente sind überwiegend in Grau- und Grüntönen.
Abbildung AS-3.2.1: Phasenverschiebung am Kondensator zwischen Spannung und Strom

AC101: Ein verlustloser Kondensator wird an eine Wechselspannungsquelle angeschlossen. Welche Phasenverschiebung zwischen Spannung und Strom stellt sich ein?

A: Der Strom eilt der Spannung um 90 ° voraus.

B: Der Strom eilt der Spannung um 45 ° voraus.

C: Die Spannung eilt dem Strom um 45 ° voraus.

D: Die Spannung eilt dem Strom um 90 ° voraus.

Wirkleistung

Der folgende Alt-Text wurde noch nicht geprüft: Kurzfassung: Diagramm mit drei sinusförmigen Kurven über der Zeit t; eine blaue, eine orange und eine grüne Kurve, zu denen rechts oben eine Legende mit den Beschriftungen „P“, „I“ und „U“ gehört; die grüne Kurve ist zusätzlich halbtransparent schattiert. Detailbeschreibung: Ein kartesisches Koordinatensystem zeigt eine horizontale Achse mit Pfeil nach rechts und der Beschriftung „t“ sowie eine vertikale Achse mit Pfeil nach oben; es gibt kurze, unbeschriftete Teilstriche, aber keine Zahlenwerte. Rechts oben steht eine Legende: ein kurzer grüner Linienzug mit „P“, ein orangefarbener Linienzug mit „I“ und ein blauer Linienzug mit „U“. Drei glatte Sinuskurven verlaufen über die Breite: Die blaue Kurve hat die größte Amplitude und die längste Wellenlänge; sie startet links nahe bei Null und steigt an. Die orange Kurve hat etwas kleinere Amplitude und eine ähnliche Wellenlänge wie die blaue, ist jedoch phasenverschoben; links befindet sie sich über der Nulllinie und fällt ab, während die blaue steigt. Die grüne Kurve hat die kleinste Amplitude und eine kürzere Wellenlänge (sie schwingt häufiger als die blaue und orange Kurve); die Fläche zwischen der grünen Kurve und der horizontalen Nulllinie ist halbtransparent grün schattiert, sowohl oberhalb als auch unterhalb der Nulllinie, entsprechend dem Vorzeichen der Kurve.
Abbildung AS-3.2.2: Das Produkt von U × I ergibt die grüne Leistungskurve

AC111: An einem Kondensator mit einer Kapazität von 1 μF wird ein NF-Signal mit 10 kHz und 12 V$_{\textrm{eff}}$ angelegt. Wie groß ist die aufgenommene Wirkleistung im eingeschwungenen Zustand?

A: 0,75 W

B: 9 W

C: 0,9 W

D: Näherungsweise 0 W

  • Wirkleistung wird nur in einem ohmschen Widerstand umgesetzt (Strom und Spannung in Phase)
  • Blindwiderstand nimmt keine Wirkenergie auf
  • Wird deshalb nicht warm
  • Ein warmer Kondensator bei Hochfrequenz hat einen ohmschen Anteil und sollte ersetzt werden
AC103: Welcher der folgenden Widerstände hat keine Wärmeverluste?

A: Der Blindwiderstand

B: Der NTC-Widerstand

C: Der Wirkwiderstand

D: Der Metalloxidwiderstand

Kapazitiver Blindwiderstand $X_{\textrm{C}}$

Kondensator wird an Wechselspannung angeschlossen ständig geladen und entladen → Wechselstromwiderstand / kapazitiver Blindwiderstand

  1. Wenn die Frequenz der Wechselspannung an einem Kondensator erhöht wird, dann fließt mehr Strom; dies bedeutet, der kapazitive Blindwiderstand ist kleiner geworden.
  1. Wenn die Kapazität des Kondensators erhöht wird, dann steigt auch der Strom, d. h. der Blindwiderstand wird auch kleiner.
$$X_{\textrm{C}} = \frac{1}{\omega \cdot C} = \frac{1}{2\pi \cdot f \cdot C}$$
AC102: Welches Vorzeichen hat der Blindwiderstand eines idealen Kondensators und von welchen physikalischen Größen hängt er ab? Der Blindwiderstand ist ...

A: positiv und abhängig von der Kapazität und der anliegenden Frequenz.

B: positiv und unabhängig von der Kapazität und der anliegenden Frequenz.

C: negativ und abhängig von der Kapazität und der anliegenden Frequenz.

D: negativ und unabhängig von der Kapazität und der anliegenden Frequenz.

AC104: Wie groß ist der Betrag des kapazitiven Blindwiderstands eines Kondensators mit 10 pF bei einer Frequenz von 100 MHz?

A: 31,8 Ohm

B: 318 Ohm

C: 159 Ohm

D: 1,59 kOhm

Lösungsweg

  • gegeben: $C = 10 pF$
  • gegeben: $f = 100 MHz$
  • gesucht: $X_{\textrm{C}}$
$$\begin{equation}\begin{split}\nonumber X_{\textrm{C}} &= \frac{1}{\omega \cdot C} = \frac{1}{2\pi \cdot f \cdot C}\\ &= \frac{1}{2\pi \cdot 100MHz \cdot 10pF}\\ &\approx 159\Omega \end{split}\end{equation}$$
AC105: Wie groß ist der Betrag des kapazitiven Blindwiderstands eines Kondensators mit 50 pF bei einer Frequenz von 145 MHz ?

A: ca. 18,2 kOhm

B: ca. 0,045 Ohm

C: ca. 69 Ohm

D: ca. 22 Ohm

Lösungsweg

  • gegeben: $C = 50 pF$
  • gegeben: $f = 145 MHz$
  • gesucht: $X_{\textrm{C}}$
$$\begin{equation}\begin{split}\nonumber X_{\textrm{C}} &= \frac{1}{\omega \cdot C} = \frac{1}{2\pi \cdot f \cdot C}\\ &= \frac{1}{2\pi \cdot 145MHz \cdot 50pF}\\ &\approx 22\Omega \end{split}\end{equation}$$
AC106: Wie groß ist der Betrag des kapazitiven Blindwiderstands eines Kondensators mit 100 pF bei einer Frequenz von 100 MHz?

A: ca. 15,9 Ohm

B: ca. 3,2 Ohm

C: ca. 159 Ohm

D: ca. 31,8 Ohm

Lösungsweg

  • gegeben: $C = 100 pF$
  • gegeben: $f = 100 MHz$
  • gesucht: $X_{\textrm{C}}$
$$\begin{equation}\begin{split}\nonumber X_{\textrm{C}} &= \frac{1}{\omega \cdot C} = \frac{1}{2\pi \cdot f \cdot C}\\ &= \frac{1}{2\pi \cdot 100MHz \cdot 100pF}\\ &\approx 15,9\Omega \end{split}\end{equation}$$
AC107: Wie groß ist der Betrag des kapazitiven Blindwiderstands eines Kondensators mit 100 pF bei einer Frequenz von 435 MHz ?

A: ca. 0,27 Ohm

B: ca. 27,3 kOhm

C: ca. 3,7 Ohm

D: ca. 11,5 Ohm

Lösungsweg

  • gegeben: $C = 100 pF$
  • gegeben: $f = 435 MHz$
  • gesucht: $X_{\textrm{C}}$
$$\begin{equation}\begin{split}\nonumber X_{\textrm{C}} &= \frac{1}{\omega \cdot C} = \frac{1}{2\pi \cdot f \cdot C}\\ &= \frac{1}{2\pi \cdot 435MHz \cdot 100pF}\\ &\approx 3,7\Omega \end{split}\end{equation}$$
AC108: An einem unbekannten Kondensator liegt eine Wechselspannung mit 16 V und 50 Hz. Es wird ein Strom von 32 mA gemessen. Welche Kapazität hat der Kondensator?

A: ca. 6,37 μF

B: ca. 0,45 μF

C: ca. 0,637 μF

D: ca. 4,5 μF

Lösungsweg

  • gegeben: $U = 16 V$
  • gegeben: $I = 32 mA$
$$X_{\textrm{C}} = \frac{U}{I} = \frac{16V}{32mA} = 500\Omega$$
$$\begin{equation}\begin{align}\nonumber X_{\textrm{C}} &= \frac{1}{\omega \cdot C} \\ \nonumber \Rightarrow C &= \frac{1}{\omega \cdot X_{\textrm{C}}} = \frac{1}{2\pi \cdot f \cdot X_{\textrm{C}}}\\ \nonumber &= \frac{1}{2\pi \cdot 50Hz \cdot 500\Omega}\\ \nonumber &\approx 6,37\mu F\end{align}\end{equation}$$

Kondensatorverluste

Der folgende Alt-Text wurde noch nicht geprüft: 1) Kurzfassung: Schemazeichnung eines realen Kondensators mit parallel geschaltetem Isolationswiderstand sowie in Serie angeordnetem Widerstand und einer Induktivität, begleitet von erklärendem Text. 2) Detaillierte Beschreibung: Auf weißem Hintergrund steht oben groß „Ersatzschaltbild eines realen Kondensators!“. Rechts daneben/ darunter steht in Klammern „(Equivalent Series Resistance)“, wobei „ESR“ farblich hervorgehoben und wellig unterstrichen ist. Links zeigt ein Schaltbild zwei Anschlussklemmen mit einem Kondensatorsymbol „C“, parallel dazu ein Widerstand mit der Beschriftung „Risol“; dieser Teil ist mit einem roten Kreis markiert. Rechts davon sind in Serie ein Widerstand „RESR“ und eine Spule „LESL“ angeordnet; dieser Teil ist mit einem blauen Kreis markiert. Unten rechts erscheint roter Text: „Ideal: tan δ = 0 bei ESR = 0 Ω!“. Alle Schaltlinien und Bauteilsymbole sind schwarz.
Abbildung AS-3.2.3: Ersatzschaltbild eines realen Kondensators mit einem seriellen Verlustwiderstand (ESR).

AC109: Kommt es in einem von Wechselstrom durchflossenen realen Kondensator zu Verlusten?

A: Nein, beim Kondensator handelt es sich um eine reine Blindleistung.

B: Ja, infolge des Blindwiderstands

C: Ja, infolge von Verlusten in Dielektrikum und Zuleitung

D: Nein, bei Wechselstrom treten keine Verluste auf.

AC110: Neben dem kapazitiven Blindwiderstand treten im von Wechselstrom durchflossenen Kondensator auch Verluste auf, die rechnerisch in einem parallelgeschalteten Verlustwiderstand zusammengefasst werden können. Die Kondensatorverluste werden oft durch ...

A: den relativen Verlustwiderstand in Ohm pro Farad angegeben, mit dem die Kondensatorgüte berechnet werden kann.

B: den relativen Blindwiderstand in Ohm pro Farad angegeben, mit dem die Kondensatorgüte berechnet werden kann.

C: den Verlustfaktor tan $\delta$ angegeben, der dem Kehrwert des Gütefaktors entspricht.

D: den Verlustfaktor cos $\phi$ angegeben, der dem Kehrwert des Gütefaktors entspricht.

Spule II

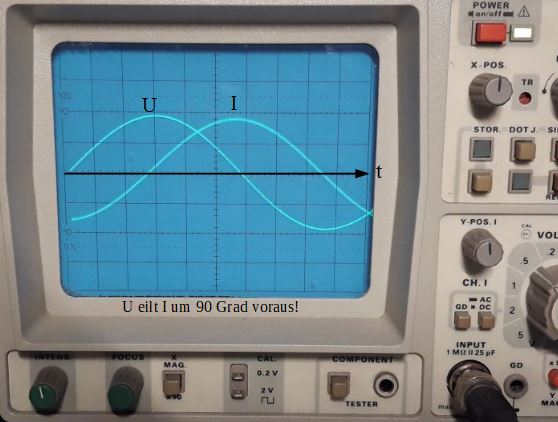
Der folgende Alt-Text wurde noch nicht geprüft: 1) Kurze Zusammenfassung: Ein analoges Oszilloskop zeigt auf einem blauen Gitter zwei phasenverschobene Sinuskurven mit den Beschriftungen „U“ und „I“, daneben sind diverse Bedienelemente und ein BNC‑Eingang sichtbar. 2) Detaillierte Beschreibung: Das Gerät ist beige/grau, links die rechteckige Bildröhre mit blauem Graticule. Auf dem Schirm verlaufen zwei helle, cyanfarbene Sinuskurven mit gleicher Amplitude; über den Kurven stehen die Buchstaben „U“ (links) und „I“ (rechts). Eine schwarze horizontale Linie mit Pfeil nach rechts trägt die Beschriftung „t“. Unterhalb des Bildschirms steht in kleiner Schrift „U eilt I um 90 Grad voraus!“. Rechts neben dem Schirm befindet sich ein Bedienfeld mit Drehknöpfen, Schaltern und Tastern; gut lesbar sind u. a. „Y-POS. I“, „CH.1“ mit einem Kippschalter „AC / GD / DC“, sowie unten ein Anschlussfeld „INPUT 1 MΩ 25 pF“ mit BNC-Buchse. Unter dem Schirm sind weitere Regler mit Beschriftungen wie „FOCUS“, „INTEN“, „CAL 0.2V / 2V“ und ein Bereich „COMPONENT TESTER“. Die Front enthält mehrere Skalenringe, Kippschalter und farbige Tasten, insgesamt deutet alles auf ein klassisches, analoges Messgerät.
Abbildung AS-3.3.1: Phasenverschiebung an einer Spule zwischen Spannung und Strom

AC201: In einer idealen Induktivität, die an einer Wechselspannungsquelle angeschlossen ist, eilt der Strom der angelegten Spannung ...

A: um 45 ° voraus.

B: um 90 ° voraus.

C: um 45 ° nach.

D: um 90 ° nach.

Wirkleistung

Der folgende Alt-Text wurde noch nicht geprüft: 1) Kurzzusammenfassung: Drei sinusförmige Kurven mit den Legenden U (blau), I (orange) und P (grün) sind über der Zeitachse t dargestellt; die Fläche zwischen der grünen Kurve und der Nulllinie ist abwechselnd ober- und unterhalb schattiert. 2) Detaillierte Beschreibung: Ein kartesisches Koordinatensystem mit vertikaler Achse (Pfeil nach oben) und horizontaler Achse (Pfeil nach rechts) zeigt in der Mitte eine durchgehende horizontale Nulllinie; rechts neben dem Pfeil der Horizontalachse steht kursiv t. Im rechten oberen Bildbereich befindet sich eine Legende: ein grüner Linienstrich mit der Beschriftung P, ein orangefarbener mit I und ein blauer mit U (alle kursiv). Über die gesamte Breite verlaufen drei glatte Sinuskurven: Die blaue Kurve U besitzt die größte Amplitude und die längste Wellenlänge (etwa eineinhalb Perioden im Bild), die orange Kurve I hat kleinere Amplitude und ist gegenüber U phasenverschoben, und die grüne Kurve P hat die kleinste Amplitude und ungefähr die doppelte Frequenz der blauen (sie zeigt etwa drei Perioden im Bild). Die grüne Kurve schneidet die Nulllinie mehrfach; die Fläche zwischen der grünen Kurve und der Nulllinie ist halbtransparent grün gefüllt, sowohl oberhalb als auch unterhalb der Nulllinie, wodurch sich abwechselnde, linsenförmige Schattierungen ergeben.
Abbildung AS-3.3.2: Das Produkt von U × I ergibt die grüne Leistungskurve

  • Blindwiderstand nimmt keine Wirkenergie auf
  • Eine ideale Spule wird nicht warm
  • Jedoch besteht eine Spule aus Draht und hat dadurch ohmsche Verluste
  • Zusätzlich wirkt der Skin-Effekt
AC202: Welches Vorzeichen hat der Blindwiderstand einer idealen Spule und von welchen physikalischen Größen hängt er ab? Der Blindwiderstand ist ...

A: positiv und unabhängig von der Induktivität und der anliegenden Frequenz.

B: negativ und abhängig von der Induktivität und der anliegenden Frequenz.

C: positiv und abhängig von der Induktivität und der anliegenden Frequenz.

D: negativ und unabhängig von der Induktivität und der anliegenden Frequenz.

Induktiver Blindwiderstand $X_{\textrm{L}}$

Spule dreht an Wechselspannung angeschlossen ständig das magnetische Feld → Wechselstromwiderstand / induktiver Blindwiderstand

  1. Wenn die Frequenz der Wechselspannung an einer Spule erhöht wird, dann fließt weniger Strom; dies bedeutet, der induktive Blindwiderstand ist größer geworden.
  2. Wenn die Induktivität der Spule erhöht wird, dann verringert sich auch der Strom, d. h. der Blindwiderstand wird auch größer.
$$X_{\textrm{L}} = \omega \cdot L = 2\pi \cdot f \cdot L$$
AC203: Beim Anlegen einer Gleichspannung $U$ = 1 V an eine Spule messen Sie einen Strom. Wird der Strom beim Anlegen von einer Wechselspannung mit $U_{\textrm{eff}}$ = 1 V größer oder kleiner?

A: Beim Betrieb mit Gleichspannung wirkt nur der Gleichstromwiderstand der Spule. Beim Betrieb mit Wechselspannung wirkt nur der kleinere induktive Widerstand $X_{\textrm{L}}$. Der Strom wird größer.

B: Beim Betrieb mit Gleich- oder Wechselspannung wirkt nur der ohmsche Widerstand $X_{\textrm{L}}$ der Spule. Der Strom bleibt gleich.

C: Beim Betrieb mit Wechselspannung wirkt nur der Wechselstromwiderstand der Spule. Beim Betrieb mit Gleichspannung wird nur der ohmsche Widerstand $X_{\textrm{L}}$ wirksam. Der Strom wird größer.

D: Beim Betrieb mit Gleichspannung wirkt nur der Gleichstromwiderstand der Spule. Beim Betrieb mit Wechselspannung wird der induktive Widerstand $X_{\textrm{L}}$ wirksam und erhöht den Gesamtwiderstand. Der Strom wird kleiner.

AC204: Wie groß ist der Betrag des induktiven Blindwiderstands einer Spule mit 3 μH Induktivität bei einer Frequenz von 100 MHz?

A: ca. 1885 Ohm

B: ca. 1,942 Ohm

C: ca. 942,0 Ohm

D: ca. 1885 kOhm

Lösungsweg

  • gegeben: $L = 3\mu H$
  • gegeben: $f = 100 MHz$
  • gesucht: $X_{\textrm{L}}$
$$\begin{equation}\begin{split}\nonumber X_{\textrm{L}} &= \omega \cdot L = 2\pi \cdot f \cdot L\\ &= 2\pi \cdot 100MHz \cdot 3\mu H\\ &\approx 1885\Omega \end{split}\end{equation}$$

Steigerung der Induktivität

Zylinderspule

$$L = \dfrac{\mu_0 \cdot \mu_r \cdot N^2 \cdot A_S}{l}$$
  • Windungszahl $N$ erhöhen
  • Spulenlänge $l$ verkürzen
  • Querschnittsfläche $A_S$ der Spule vergrößern
AC211: Das folgende Bild zeigt einen Kern, um den ein Kabel für den Bau einer Drossel gewickelt ist. Der Kern sollte üblicherweise aus ...

A: Ferrit bestehen.

B: diamagnetischem Material bestehen.

C: Stahl bestehen.

D: Kunststoff bestehen.

AC205: Wie groß ist die Induktivität einer Spule mit 14 Windungen, die auf einen Kern mit einer Induktivitätskonstante ($A_{\textrm{L}}$-Wert) von 1,5 nH gewickelt ist?

A: 2,94 nH

B: 2,94 μH

C: 29,4 nH

D: 0,294 μH

Lösungsweg

  • gegeben: $N = 14$
  • gegeben: $A_{\textrm{L}} = 1,5 nH$
  • gesucht: $L$
$$\begin{equation}\begin{split}\nonumber L &= N^2 \cdot A_{\textrm{L}}\\ &= 14^2 \cdot 1,5nH\\ &= 0,294\mu H \end{split}\end{equation}$$
AC206: Wie groß ist die Induktivität einer Spule mit 300 Windungen, die auf einen Kern mit einer Induktivitätskonstante ($A_{\textrm{L}}$-Wert) von 1250 nH gewickelt ist?

A: 112,5 μH

B: 11,25 mH

C: 1,125 mH

D: 112,5 mH

Lösungsweg

  • gegeben: $N = 300$
  • gegeben: $A_{\textrm{L}} = 1250 nH$
  • gesucht: $L$
$$\begin{equation}\begin{split}\nonumber L &= N^2 \cdot A_{\textrm{L}}\\ &= 300^2 \cdot 1250nH\\ &= 112,5mH \end{split}\end{equation}$$
AC207: Mit einem Ringkern, dessen Induktivitätskonstante ($A_{\textrm{L}}$-Wert) mit 250 nH angegeben ist, soll eine Spule mit einer Induktivität von 2 mH hergestellt werden. Wie groß ist die erforderliche Windungszahl etwa?

A: 2828

B: 3

C: 89

D: 53

Lösungsweg

  • gegeben: $L = 2 mH$
  • gegeben: $A_{\textrm{L}} = 250 nH$
  • gesucht: $N$
$$\begin{equation}\begin{align}\nonumber L &= N^2 \cdot A_{\textrm{L}}\\ \nonumber N &= \sqrt{\frac{L}{A_{\textrm{L}}}} = \sqrt{\frac{2mH}{250nH}} \\ \nonumber &= 89\ \textrm{Windungen} \end{align}\end{equation}$$
AC208: Ein Spulenkern hat eine Induktivitätskonstante ($A_{\textrm{L}}$-Wert) von 30 nH. Wie groß ist die erforderliche Windungszahl zur Herstellung einer Induktivität von 12 μH in etwa?

A: 6

B: 400

C: 360

D: 20

Lösungsweg

  • gegeben: $L = 12\mu H$
  • gegeben: $A_{\textrm{L}} = 30 nH$
  • gesucht: $N$
$$\begin{equation}\begin{align}\nonumber L &= N^2 \cdot A_{\textrm{L}}\\ \nonumber N &= \sqrt{\frac{L}{A_{\textrm{L}}}} = \sqrt{\frac{12\mu H}{30nH}} \\ \nonumber &= 20\ \textrm{Windungen} \end{align}\end{equation}$$

Spulenverluste

  • Verlustfaktor $\tan(\delta) = \frac{R}{X_L}$
  • Verluste im Leiter
AC209: Neben dem induktiven Blindwiderstand treten in der mit Wechselstrom durchflossenen Spule auch Verluste auf, die rechnerisch in einem seriellen Verlustwiderstand zusammengefasst werden können. Als Maß für die Verluste in einer Spule wird auch ...

A: der relative Blindwiderstand in Ohm pro Henry angegeben, mit dem die Spulengüte berechnet werden kann.

B: der relative Verlustwiderstand in Ohm pro Henry angegeben, mit dem die Spulengüte berechnet werden kann.

C: der Verlustfaktor tan $\delta$ angegeben, der dem Kehrwert des Gütefaktors entspricht.

D: der Verlustfaktor cos $\varphi$ angegeben, der dem Kehrwert des Gütefaktors entspricht.

Scheinwiderstand

  • Reihenschaltung von Blindwiderstand und Wirkwiderstand → Scheinwiderstand $Z$
  • Tritt nur bei Wechselspannung auf
  • Kann nicht mit einem Ohm-Meter gemessen werden
  • Spule in der Funktechnik → Impedanz
  • Antennenimpedanz, Eingangs- und Ausgangsimpedanz, Impedanzwandler, …
  • Impedanz Z in Ω

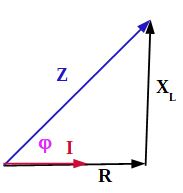
Der folgende Alt-Text wurde noch nicht geprüft: Kurzfassung: Vektordiagramm eines rechtwinkligen Impedanzdreiecks mit den Achsen R und X_L, dem diagonalen Zeiger Z sowie den Markierungen I und φ. Detailbeschreibung: Unten verläuft eine schwarze horizontale Achse nach rechts, mit der Beschriftung R; am rechten Ende steht eine schwarze vertikale Achse nach oben, beschriftet X_L. Vom linken unteren Eckpunkt führt eine blaue Diagonale mit Pfeilspitze schräg nach oben rechts zur Spitze der vertikalen Achse und ist mit Z gekennzeichnet. Auf der unteren Horizontalen liegt ein roter Pfeil nach rechts, beschriftet I. Zwischen der roten Horizontalen und der blauen Diagonalen ist am linken Eck der Winkel φ in Magenta eingezeichnet.
Abbildung AS-3.3.3: Geometrische Addition von $R$ und $X_L$ und Phasenverschiebung zwischen $Z$ und $R$

$$Z = \sqrt{R^2 + X^2}$$
AA101: Welche Einheit wird üblicherweise für die Impedanz verwendet?

A: Farad

B: Siemens

C: Ohm

D: Henry

Abschirmung von elektrischen Feldern

Ein Gehäuse aus einem magnetisch gut leitfähigem Material.

AC210: Um die Abstrahlungen der Spule eines abgestimmten Schwingkreises zu verringern, sollte die Spule ...

A: in einem isolierenden Kunststoffgehäuse untergebracht werden.

B: einen abgestimmten Kunststoffkern aufweisen.

C: einen hohlen Kupferkern aufweisen.

D: in einem leitenden Metallgehäuse untergebracht werden.

Übertrager II

Transformator-Prinzip

Der folgende Alt-Text wurde noch nicht geprüft: Kurzbeschreibung: Ein Transformator mit zwei Wicklungen und seitlichen Anschlussleisten, von oben auf weißem Hintergrund fotografiert. Detaillierte Beschreibung: Das Gerät besteht aus einem rechteckigen Blechkern mit zwei nebeneinander liegenden Spulenkörpern, die mit blaugrünem Isoliermaterial umwickelt sind. Auf der oberen Spule klebt mittig ein gelber Streifen, auf der unteren Spule ein hellblaues Etikett mit der Aufschrift „Trafo SU 60 b“ und „Material-Nr. 31-024“. An beiden Stirnseiten befinden sich helle Kunststoffträger mit Reihen von metallischen Lötfahnen; daran sind feine, lackierte Kupferdrähte angeschlossen, teils mit sichtbaren Lötstellen und leichten Anlaufspuren. Links führen zwei rote flexible Leitungen zu einer Anschlussseite; daneben ist ein kleines blaues zylindrisches Element zu sehen. Unten sind Montagewinkel mit Schrauben erkennbar. Der Hintergrund ist einheitlich weiß, das Foto zeigt das Bauteil leicht von oben.
Abbildung AS-3.4.1: Trafo mit sichtbar getrennten Wicklungen

AC301: Durch Gegeninduktion wird in einer Spule eine Spannung erzeugt, wenn ...

A: ein veränderlicher Strom durch eine magnetisch gekoppelte benachbarte Spule fließt.

B: ein konstanter Gleichstrom durch eine magnetisch gekoppelte benachbarte Spule fließt.

C: ein veränderlicher Strom durch die Spule fließt und sich dabei ein dielektrischer Gegenstand innerhalb der Spule befindet.

D: sich die Spule in einem konstanten Magnetfeld befindet.

Das Verhältnis der Windungen zwischen Primär- und Sekundärseite ist wie das Verhältins der Spannung zwischen Primär- zu Sekundärseite, aber wie das Verhältnis der Ströme zwischen Sekundär- zu Primärseite:

$$ü = \frac{N_P}{N_S} = \frac{U_P}{U_S} = \frac{I_S}{I_P}$$

Das Verhältnis der Primär- zur Sekundärimpedanz ist wie die obigen Verhältnisse zum Quadrat:

$$ü = \frac{Z_P}{Z_S} = (\frac{N_P}{N_S})^2 = (\frac{U_P}{U_S})^2 = (\frac{I_S}{I_P})^2$$

Oder nach Ziehung der Wurzel:

$$ü = \frac{N_P}{N_S} = \frac{U_P}{U_S} = \frac{I_S}{I_P} = \sqrt{\frac{Z_P}{Z_S}}$$
AC302: Ein Transformator setzt die Spannung von 230 V auf 6 V herunter und liefert dabei einen Strom von 1,15 A. Wie groß ist der dadurch in der Primärwicklung zu erwartende Strom bei Vernachlässigung der Verluste?

A: 0,83 mA

B: 22,7 mA

C: 33,3 mA

D: 30 mA

Lösungsweg

  • gegeben: $U_P = 230 V$
  • gegeben: $U_S = 6 V$
  • gegeben: $I_S = 1,15 A$
  • gesucht: $I_P$
$$\begin{equation}\begin{align} \nonumber \frac{U_P}{U_S} &= \frac{I_S}{I_P} \\ \nonumber \Rightarrow I_P &= \frac{I_S \cdot U_S}{U_P} = \frac{1,15A \cdot 6V}{230V} \\ \nonumber &= 30mA \end{align}\end{equation}$$
AC303: In dieser Schaltung beträgt $R$=16 kOhm. Die Impedanz zwischen den Anschlüssen a und b beträgt im Idealfall ...

A: 16 kOhm.

B: 4 kOhm.

C: 64 kOhm.

D: 1 kOhm.

Lösungsweg

  • gegeben: $Z_S = 16k\Omega$
  • gegeben: $ü = \frac{1}{4}$
  • gesucht: $Z_P$
$$\begin{equation}\begin{align} \nonumber ü &= \sqrt{\frac{Z_P}{Z_S}} \\ \nonumber \Rightarrow Z_P &= ü^2 \cdot Z_S = \frac{1^2}{4^2} \cdot 16k\Omega \\ \nonumber &= \frac{16k\Omega}{16} = 1k\Omega \end{align}\end{equation}$$
AC304: In dieser Schaltung beträgt $R$=6,4 kOhm. Die Impedanz zwischen den Anschlüssen a und b beträgt im Idealfall ...

A: 6,4 kOhm.

B: 1,6 kOhm.

C: 26 kOhm.

D: 0,4 kOhm.

Lösungsweg

  • gegeben: $Z_S = 6,4k\Omega$
  • gegeben: $ü = \frac{1}{4}$
  • gesucht: $Z_P$
$$\begin{equation}\begin{align} \nonumber ü &= \sqrt{\frac{Z_P}{Z_S}} \\ \nonumber \Rightarrow Z_P &= ü^2 \cdot Z_S = \frac{1^2}{4^2} \cdot 6,4k\Omega \\ \nonumber &= \frac{6,4k\Omega}{16} = 0,4k\Omega \end{align}\end{equation}$$
AC305: Für die Anpassung einer Antenne mit einem Fußpunktwiderstand von 450 Ohm an eine 50 Ohm-Übertragungsleitung sollte ein Übertrager mit einem Windungsverhältnis von ...

A: 9:1 verwendet werden.

B: 3:1 verwendet werden.

C: 4:1 verwendet werden.

D: 16:1 verwendet werden.

Lösungsweg

  • gegeben: $Z_P = 450\Omega$
  • gegeben: $Z_S = 50\Omega$
  • gesucht: $ü$
$$\begin{equation}\begin{split} \nonumber ü &= \sqrt{\frac{Z_P}{Z_S}} = \sqrt{\frac{450\Omega}{50\Omega}} \\ &= \sqrt{\frac{9}{1}} = \frac{3}{1} \end{split}\end{equation}$$
AC306: Für die Anpassung einer 50 Ohm Übertragungsleitung an eine endgespeiste Halbwellenantenne mit einem Fußpunktwiderstand von 2,5 kOhm wird ein Übertrager verwendet. Er sollte in etwa ein Windungverhältnis von ...

A: 1:3 aufweisen.

B: 1:49 aufweisen.

C: 1:7 aufweisen.

D: 1:14 aufweisen.

Lösungsweg

  • gegeben: $Z_P = 50\Omega$
  • gegeben: $Z_S = 2,5k\Omega$
  • gesucht: $ü$
$$\begin{equation}\begin{split} \nonumber ü &= \sqrt{\frac{Z_P}{Z_S}} = \sqrt{\frac{50\Omega}{2,5k\Omega}} \\ &= \sqrt{\frac{1}{50}} \approx \frac{1}{7} \end{split}\end{equation}$$

Maximaler Strom

  • Leitung darf nicht zu warm werden
  • Sonst schmilzt die Isolation
  • Oder der Leiter glüht
  • → zulässige Stromdichte in Stromstärke bezogen auf den Leiterquerschnitt

Beispiele zulässige Stromdichte

nach VDE

  • Frei verlegte Leiter aus Kupfer: $\frac{12 A}{0,75 mm^2}$
  • Schmelzsicherungen: bis zu $3000\frac{A}{mm^2}$
  • Transformatoren: $2,5\frac{A}{mm^2}$ (schlechte Wärmeabstrahlung der Wicklungen)
AC307: Eine Transformatorwicklung hat einen Drahtdurchmesser von 0,5 mm. Die zulässige Stromdichte beträgt 2,5 A/mm². Wie groß ist der zulässige Strom?

A: ca. 0,19 A

B: ca. 0,49 A

C: ca. 1,96 A

D: ca. 1,25 A

Lösungsweg

  • gegeben: $d = 0,5 mm$
  • gegeben: Stromdichte $\frac{I}{A} = \frac{2,5 A}{1 mm^2}$
  • gesucht: $I_{max}$
$$A_{Dr} = \frac{d^2 \cdot \pi}{4} = \frac{(0,5mm)^2 \cdot \pi}{4} \approx 0,196mm^2$$
$$I_{max} = \frac{I}{A} \cdot A_{Dr} = \frac{2,5A}{1mm^2} \cdot 0,196mm^2 = 0,49A$$

Halbleiter II

Halbleiter

  • Bestehen aus einer Gitterstruktur
  • 4 geteilte Elektronen auf der äußeren Schale
  • Sind eigentlich Isolatoren
  • Können durch Temperaturanstieg, Licht oder Dotierung zu Leitern werden
AB104: Was versteht man unter Halbleitermaterialien?

A: Einige Stoffe (z. B. Silizium) sind in reinem Zustand bei Raumtemperatur gute Leiter. Durch geringfügige Zusätze von geeigneten anderen Stoffen (z. B. Bismut, Tellur) fällt ihr Widerstand auf den halben Wert.

B: Einige Stoffe (z. B. Silizium) sind in reinem Zustand bei Raumtemperatur gute Leiter. Durch geringfügige Zusätze von geeigneten anderen Stoffen (z. B. Bor, Phosphor) oder bei hohen Temperaturen nimmt jedoch ihre Leitfähigkeit ab.

C: Einige Stoffe (z. B. Silizium) sind in reinem Zustand bei Raumtemperatur gute Isolatoren. Durch geringfügige Zusätze von geeigneten anderen Stoffen (z. B. Bor, Phosphor) oder bei hohen Temperaturen werden sie jedoch zu Leitern.

D: Einige Stoffe (z. B. Silizium) sind in reinem Zustand bei Raumtemperatur gute Elektrolyten. Durch geringfügige Zusätze von geeigneten anderen Stoffen (z. B. Bismut, Tellur) kann man daraus entweder N-leitendes- oder P-leitendes Material für Anoden bzw. Kathoden von Batterien herstellen.

Dotierung

  • „Verunreinigung“ der Halbleiter
  • Stoffe mit 5 Elektronen auf der äußeren Schale → Elektronenüberschuss → n-Dotierung
  • Stoffe mit 3 Elektronen auf der äußeren Schale → Elektronenmangel („Loch“) → p-Dotierung

Der folgende Alt-Text wurde noch nicht geprüft: Kurzzusammenfassung: Schematische Rastergrafik mit neun Knotenpunkten; an acht Knoten steht „Si“ und am mittleren Knoten „P“, jeweils in grauen Kreisen mit kleinen blauen Punkten darum. Detaillierte Beschreibung: Ein quadratisches 3×3-Raster aus senkrechten und waagerechten, grau gestrichelten Linien. An jedem der neun Kreuzungspunkte befindet sich ein hellgrauer Kreis mit schwarzer Beschriftung. In acht Kreisen steht „Si“ (oben links, oben Mitte, oben rechts; Mitte links, Mitte rechts; unten links, unten Mitte, unten rechts). Im mittleren Kreis steht „P“. Um jeden „Si“-Kreis sind vier kleine blaue Punkte gleichmäßig auf dem Kreis verteilt (oben, rechts, unten, links). Um den „P“-Kreis sind insgesamt fünf blaue Punkte zu sehen: vier davon wie bei den „Si“-Kreisen auf den Kardinalpositionen am Kreis, plus ein zusätzlicher kleiner blauer Punkt knapp rechts außerhalb des Kreises. Die Hintergrundfläche ist weiß.
Abbildung AS-3.5.2: n-Dotierung mit Phosphor

AB105: Was versteht man unter Dotierung?

A: Das Entfernen von Verunreinigungen aus einem Halbleitergrundstoff, um Elektronen zu generieren.

B: Das Einbringen von magnetischen Nord- oder Südpolen in einen Halbleitergrundstoff, um die Induktivität zu erhöhen.

C: Das Einbringen von chemisch anderswertigen Fremdatomen in einen Halbleitergrundstoff, um freie Ladungsträger zur Verfügung zu stellen.

D: Das Entfernen von Atomen aus dem Halbleitergrundstoff, um die elektrische Leitfähigkeit zu senken.

AB106: N-leitendes Halbleitermaterial ist gekennzeichnet durch ...

A: einen Überschuss an beweglichen Elektronen.

B: einen Überschuss an beweglichen Elektronenlöchern.

C: ein Fehlen von Atomen im Gitter des Halbleiterkristalls.

D: ein Fehlen von Dotierungsatomen.

AB107: P-leitendes Halbleitermaterial ist gekennzeichnet durch ...

A: einen Überschuss an beweglichen Elektronenlöchern.

B: einen Überschuss an beweglichen Elektronen.

C: ein Fehlen von Atomen im Gitter des Halbleiterkristalls.

D: ein Fehlen von Dotierungsatomen.

Kombination

Der folgende Alt-Text wurde noch nicht geprüft: Kurzfassung: Schematische Darstellung einer PN-Grenzschicht mit den Beschriftungen „P“, „Diffusion“ und „N“ sowie einem Diodensymbol darunter. Detailbeschreibung: Ein horizontaler, von zwei Anschlussleitungen durchquerter Rechteckblock ist in drei Zonen geteilt: links ein rotes Feld mit der Beschriftung „P“ (oben) und sechs roten, leeren Kreisen; rechts ein blaues Feld mit der Beschriftung „N“ (oben) und sechs blauen, ausgefüllten Punkten; in der Mitte eine graue Sperrschicht mit einer dunklen, schmalen Doppellinie. Über der Mitte steht „Diffusion“. Innerhalb des Blocks zeigen ein roter waagerechter Pfeil nach rechts und ein blauer waagerechter Pfeil nach links. In der Sperrschicht sind ein blaues „−“ auf der linken Seite und ein rotes „+“ auf der rechten Seite zu sehen; darunter steht ein gelbes „E“ neben einem gelben Pfeil nach links. Unter dem Block ist das Diodensymbol dargestellt: ein nach rechts weisendes Dreieck vor einer senkrechten Linie.
Abbildung AS-3.5.4: PN-Übergang

  • n-dotierter Halbleiter an p-dotieren Halbleiter
  • Elektronen aus dem n-dotieren Gebiet wandern in das p-dotierte Gebiet → Diffusion
AB108: Das folgende Bild zeigt den prinzipiellen Aufbau einer Halbleiterdiode. Wie entsteht die Sperrschicht?

A: An der Grenzschicht wandern Elektronen aus dem P-Teil in den N-Teil. Dadurch wird auf der P-Seite der Elektronenüberschuss teilweise abgebaut, auf der N-Seite der Elektronenmangel teilweise neutralisiert. Es bildet sich auf beiden Seiten der Grenzfläche eine isolierende Schicht.

B: An der Grenzschicht wandern Elektronen aus dem N-Teil in den P-Teil. Dadurch wird auf der N-Seite der Elektronenüberschuss teilweise abgebaut, auf der P-Seite der Elektronenmangel teilweise neutralisiert. Es bildet sich auf beiden Seiten der Grenzfläche eine isolierende Schicht.

C: An der Grenzschicht wandern Atome aus dem N-Teil in den P-Teil. Dadurch wird auf der N-Seite der Atommangel abgebaut, auf der P-Seite der Atommangel vergrößert. Es bildet sich auf beiden Seiten der Grenzfläche eine leitende Schicht.

D: An der Grenzschicht wandern Atome aus dem P-Teil in den N-Teil. Dadurch wird auf der P-Seite der Atommangel abgebaut, auf der N-Seite der Atommangel vergrößert. Es bildet sich auf beiden Seiten der Grenzfläche eine leitende Schicht.

pn-Diode in Durchlassrichtung

Der folgende Alt-Text wurde noch nicht geprüft: Kurzfassung: Schematische Schaltung mit einem zweigeteilten, farbigen Rechteck oben beschriftet „P“ und „N“, einer Spannungsquelle unten und zwei Pfeilen mit den Texten „tech.“ und „phys.“ für Richtungen. Detailbeschreibung: Ein rechteckiger, geschlossener Stromkreis ist mit einer dünnen schwarzen Linie gezeichnet. Im oberen horizontalen Zweig sitzt mittig ein breites Rechteck als Bauteil, links rötlich gefärbt und mit „P“ beschriftet, rechts hellblau gefärbt und mit „N“ beschriftet; die seitlichen Leitungen gehen jeweils an die linke und rechte Seite dieses Rechtecks. Im unteren horizontalen Zweig ist in der Mitte ein Batteriesymbol (zwei parallele, vertikale Linien) eingezeichnet. Über diesem Symbol steht „U“ mit einem nach rechts gerichteten Pfeil. Links unten am Leiter steht in roter Schrift „tech.“ mit einem nach links gerichteten Pfeil, rechts unten am Leiter steht in blauer Schrift „phys.“ mit einem nach rechts gerichteten Pfeil. Hintergrund weiß, Leitungen und Umrisse schwarz.
Abbildung AS-3.5.5: PN-Übergang mit externer Spannung

  • Anlegen einer Spannung am p-Gebiet (Anode)
  • Spannung muss positiver als am n-Gebiet (Kathode) sein
AC402: Wie verhalten sich die Elektronen in einem in Durchlassrichtung betriebenen PN-Übergang?

A: Sie zerfallen beim Übergang.

B: Sie bleiben im N-Bereich.

C: Sie wandern von P nach N.

D: Sie wandern von N nach P.

pn-Diode im Sperrbetrieb

Der folgende Alt-Text wurde noch nicht geprüft: Kurzfassung: Schematische Zeichnung eines rechteckigen Stromkreises mit einem oben eingesetzten Block, der mit „P“ und „N“ beschriftet ist, und einer unten eingezeichneten Spannungsquelle mit dem Hinweis „U“ und einem Pfeil nach links. Detaillierte Beschreibung: Ein rechteckiger Leitungsrahmen bildet einen geschlossenen Stromkreis. Oben in der Mitte sitzt ein horizontaler, rechteckiger Block, der links mit „P“ und rechts mit „N“ beschriftet ist; in der Mitte verläuft eine senkrechte Trennlinie. Am linken Rand des Blocks ist ein schmaler, rötlicher Streifen, am rechten Rand ein schmaler, hellblauer Streifen; die Bereiche zwischen den farbigen Streifen und der Mittellinie sind grau. Der Block ist links und rechts mit den Leitungen des Rahmens verbunden. Unten in der Mitte liegt ein Batteriesymbol (zwei parallele vertikale Platten, links eine kürzere ausgefüllte, rechts eine längere Linie) im unteren Leiterzug. Über der Batterie steht „U“ mit einem nach links gerichteten Pfeil. Es sind keine Zahlenwerte oder Achsen angegeben.
Abbildung AS-3.5.6: PN-Übergang mit externer Spannung

  • Positive Spannung an der Kathode
AB109: Wie verhält sich die Verarmungszone in der hier dargestellten Halbleiterdiode?

A: Sie erweitert sich.

B: Sie verengt sich.

C: Sie verändert sich nicht.

D: Sie verschwindet.

Diode II

Durchlassrichtung

  • Elektronenfluss von N nach P
  • Technische Stromrichtung ist entgegengesetzt zur Richtung des Elektronenflusses
AC401: Ein in Durchlassrichtung betriebener PN-Übergang ermöglicht ...

A: die Halbierung des Stromflusses.

B: den Elektronenfluss von N nach P.

C: keinen Stromfluss.

D: den Elektronenfluss von P nach N.

Temperatur

  • Bei höherer Temperatur gibt es mehr freie Elektronen
  • Der Sättigungsstrom steigt mit steigender Temperatur
  • Aber die Beweglichkeit ändert sich
  • Dadurch sinkt die Durchlassspannung (mit ca. −2 mV/°C)
AC403: Wie verhält sich die Durchlassspannung einer Diode in Abhängigkeit von der Temperatur?

A: Die Spannung sinkt bei steigender Temperatur.

B: Die Spannung steigt bei steigender Temperatur.

C: Die Spannung oszilliert mit steigender Temperatur.

D: Die Spannung ist unabhängig von der Temperatur.

Kapazitätsdiode (Varicap)

  • Kapazitätsdiode nutzt die Kapazität über der Raumladungszone
  • Es darf kein Gleichstrom fließen
  • Wird in Sperrrichtung betrieben
AC404: Wie verhält sich die Kapazität einer Kapazitätsdiode (Varicap)?

A: Sie nimmt mit abnehmendem Durchlassstrom zu.

B: Sie nimmt mit abnehmender Sperrspannung zu.

C: Sie nimmt mit zunehmender Sperrspannung zu.

D: Sie nimmt mit zunehmendem Durchlassstrom zu.

Spannungsbegrenzung

  • Antiparallele Dioden
  • Begrenzung der Amplitude einer Wechselspannung
  • Silizium: ca. 0,6 V Schwellspannung
  • Germanium: ca. 0,3 V Schwellspannung
  • → Clipping
AC405: Das folgende Signal wird als $U_1$ an den Eingang der Schaltung mit Siliziumdioden gelegt. Wie sieht das zugehörige Ausgangssignal $U_2$ aus?
A:
B:
C:
D:
AC406: Das folgende Signal wird als $U_1$ an den Eingang der Schaltung mit Germaniumdioden gelegt. Wie sieht das zugehörige Ausgangssignal $U_2$ aus?
A:
B:
C:
D:

Fotodiode

  • Licht wird in der Raumladungszone absorbiert
  • Es entstehen Elektron-Loch-Paare
  • Elektronen bewegen sich zum p-Gebiet, Löcher zum n-Gebiet
  • Wird ein Verbraucher (mit negativer Spannung am p-Anschluss) angeschlossen, wirkt die Fotodiode als Stromquelle
  • Der Strom ist proportional zur Lichtintensität
AC407: Welches Bauteil kann durch Lichteinfall elektrischen Strom erzeugen?

A: Fotowiderstand

B: Blindwiderstand

C: Kapazitätsdiode

D: Fotodiode

Optokoppler

  • Zusammenschluss von Leuchtdiode und Fotodiode in einem Gehäuse
  • Eingangsseite: Leuchtdiode
  • Ausgangsseite: Fotodiode
  • Beide sind voneinander galvanisch getrennt
AC408: Die Hauptfunktion eines Optokopplers ist ...

A: die Signalanzeige durch Licht.

B: die galvanische Entkopplung zweier Stromkreise durch Licht.

C: die Erzeugung von Gleichstrom durch Licht.

D: die Erzeugung von hochfrequentem Wechselstrom durch Licht.

Transistor II

Bipolarer Transistor

Der folgende Alt-Text wurde noch nicht geprüft: Kurzfassung: Zwei nebeneinander stehende Transistorsymbole im Kreis, links mit der Beschriftung „NPN“, rechts „PNP“, jeweils mit den Anschlussbuchstaben „B“, „C“ und „E“. Detailbeschreibung: Auf weißem Hintergrund sind zwei identische Kreis-Symbole mit Transistordarstellungen gezeigt, links das Symbol mit der darunter stehenden Beschriftung „NPN“, rechts das Symbol mit „PNP“. Bei beiden Symbolen ist links am Kreis ein horizontaler Anschluss mit der Buchstabenbeschriftung „B“, oben ein kurzer senkrechter Anschluss mit „C“ und unten ein kurzer senkrechter Anschluss mit „E“ (die Buchstaben „B“, „C“ und „E“ sind hellgrau dargestellt). Im Inneren beider Kreise verläuft eine kurze senkrechte Linie vom linken Rand (Basis) nach innen; von dieser Linie zweigt oben eine schräge Leitung zum oberen Anschluss (Kollektor) ab und unten eine schräge Leitung zum unteren Anschluss (Emitter). Beim linken Symbol („NPN“) befindet sich am unteren schrägen Zweig ein Pfeil, der vom inneren Knoten in Richtung des unteren Anschlusses „E“ zeigt (nach außen). Beim rechten Symbol („PNP“) zeigt der Pfeil am unteren schrägen Zweig in die entgegengesetzte Richtung, also vom unteren Anschluss „E“ zum inneren Knoten (nach innen). Zwischen den beiden Symbolen ist ein deutlicher horizontaler Abstand.
Abbildung AS-3.7.1: Schaltbild eines npn- und pnp-Bipolartransistors mit Kollektor (C), Basis (B) und Emitter (E)

  • Drei Halbleiterzonen
  • Abwechselnd n- und p-dotiert
  • npn-Transistor und pnp-Transistor
AC503: Mit welchem Anschluss ist der p-dotierte Bereich eines NPN-Transistors verbunden?

A: Gehäuse

B: Basis

C: Kollektor

D: Emitter

AC504: Mit welchem Anschluss ist der n-dotierte Bereich eines PNP-Transistors verbunden?

A: Emitter

B: Kollektor

C: Gehäuse

D: Basis

Stromsteuerung und Faktor

  • Basis-Emitter-Spannung $U_{\textrm{BE}}$ steuert Kollektorstrom $I_{\textrm{C}}$ exponentiell
  • Beim Bipolartransistor fließt immer ein exponentiell von $U_{\textrm{BE}}$ abhängiger Basisstrom $I_{\textrm{B}}$
  • Faktor $B$ ist der Stromverstärkungsfaktor des Transistors
  • Liegt bei ca. 20 bis 500
$$B = \frac{I_{\textrm{C}}}{I_{\textrm{B}}}$$
AC501: Ein bipolarer Transistor ist ...

A: spannungsgesteuert.

B: stromgesteuert.

C: thermisch gesteuert.

D: feldgesteuert.

Leitender Bipolartransistor

  • Signifikanter Kollektorstrom fließt
  • Basis-Emitter-Diode in Durchlassrichtung
  • Kollektor-Basis-Diode sperrt, damit keine Ladungsträger aus dem Kollektor in die Basis gelangen
AC505: Bei einem bipolaren Transistor in leitendem Zustand befindet sich der Basis-Emitter-PN-Übergang ...

A: im Leerlauf.

B: in Durchlassrichtung.

C: im Kurzschluss.

D: in Sperrrichtung.

Rechnungen

AC515: Die Betriebsspannung beträgt 12 V, der Kollektorstrom soll 5 mA betragen, die Gleichstromverstärkung des Transistors beträgt 298. Berechnen Sie den Vorwiderstand $R_1$.

A: ca. 2,3 kOhm

B: ca. 68 kOhm

C: ca. 680 kOhm

D: ca. 715 kOhm

Lösungsweg

  • Die Größe von $R_1$ stellt den Basisstrom $I_B$ ein
  • $I_B$ ist um 298 kleiner als $I_C$
  • Für die Spannung an $R_1$ muss der Transistorverlust abgezogen werden
  • gegeben: $U = 12 V$
  • gegeben: $I_{\textrm{C}} = 5 mA$
  • gegeben: $B = 298$
  • gegeben: $U_{\textrm{BE}} = 0,6 V$
  • gesucht: $R_1$
$$B = \frac{I_{\textrm{C}}}{I_{\textrm{B}}} \Rightarrow I_{\textrm{B}} = \frac{I_{\textrm{C}}}{B} = \frac{5mA}{298} = 16,779\mu A$$
$$R_1 = \frac{U-U_{\textrm{BE}}}{I_{\textrm{B}}} = \frac{12V - 0,6V}{16,779\mu A} \approx 680k\Omega$$
AC518: Die Betriebsspannung beträgt 10 V, der Kollektorstrom soll 2 mA betragen, die Gleichstromverstärkung des Transistors beträgt 200. Durch den Querwiderstand $R_2$ soll der zehnfache Basisstrom fließen. Berechnen Sie den Vorwiderstand $R_1$.

A: ca. 940 kOhm

B: ca. 540 kOhm

C: ca. 85,5 kOhm

D: ca. 76,4 kOhm

Arbeitspunktstabilisation

Der folgende Alt-Text wurde noch nicht geprüft: Schaltplan mit einem Transistor in der Mitte, markiert mit einem Pfeil für den Strom IC. Links davon befinden sich zwei vertikale Widerstände, R1 und R2, sowie ein horizontaler Kondensator C1. Rechts oben vom Transistor ist ein weiterer Widerstand RC und rechts daneben ein Kondensator C2. Eine Spannungsquelle ist oben links eingezeichnet und zeigt positive und negative Anschlüsse. Ein Pfeil zeigt 0,6 V an einem Punkt zwischen R2 und dem Transistor.
Abbildung AS-3.7.2: Transistorschaltung mit Basisspannungsteiler

AC516: Warum soll bei dem gezeigten Basisspannungsteiler der Strom durch $R_2$ etwa 10-mal größer als der Basisstrom sein?

A: Damit sich der Basisstrom bei Erwärmung nicht ändert.

B: Damit $R_2$ eine Stromgegenkopplung bewirkt.

C: Damit $R_2$ eine Spannungsgegenkopplung bewirkt

D: Damit der Arbeitspunkt stabil bleibt.

Lösungsweg

  • gegeben: $U = 10 V$
  • gegeben: $I_{\textrm{C}} = 2 mA$
  • gegeben: $B = 200$
$$B = \frac{I_{\textrm{C}}}{I_{\textrm{B}}} \Rightarrow I_{\textrm{B}} = \frac{I_{\textrm{C}}}{B} = \frac{2mA}{200} = 10\mu A$$
$$U_{\textrm{R1}} = U - U_{\textrm{R2}} = 10V - 0,6V = 9,4V$$
$$I_{\textrm{R1}} = I_{\textrm{B}} + I_{\textrm{R2}} = I_{\textrm{B}} + 10 \cdot I_{\textrm{B}} = 110\mu A$$
$$R_1 = \frac{U_{\textrm{R1}}}{I_{\textrm{R1}}} = \frac{9,4V}{110\mu A} \approx 85,5k\Omega$$
AC517: Die Betriebsspannung beträgt 10 V, der Kollektorstrom soll 2 mA betragen, die Gleichstromverstärkung des Transistors beträgt 200. Durch den Querwiderstand $R_2$ soll der zehnfache Basisstrom fließen. Am Emitterwiderstand soll 1 V abfallen. Berechnen Sie den Vorwiderstand $R_1$.

A: ca. 76,4 kOhm

B: ca. 540 kOhm

C: ca. 85,5 kOhm

D: ca. 940 kOhm

Lösungsweg

  • $U_{\textrm{R2}}$ ist gleich groß wie $U_{\textrm{BE}} + U_{\textrm{RE}}$
  • Kollektorstrom wird vor allem durch $R_{\textrm{E}}$ festgelegt
  • Sehr stabile Schaltung
  • gegeben: $U = 10 V$
  • gegeben: $I_{\textrm{C}} = 2 mA$
  • gegeben: $B = 200$
  • gesucht: $R_1$
$$B = \frac{I_{\textrm{C}}}{I_{\textrm{B}}} \Rightarrow I_{\textrm{B}} = \frac{I_{\textrm{C}}}{B} = \frac{2mA}{200} = 10\mu A$$
$$U_{\textrm{R2}} = U_{\textrm{BE}} + U_{R_{\textrm{E}}} = 0,6V + 1V = 1,6V$$
$$U_{\textrm{R1}} = U - U_{\textrm{R2}} = 10V - 1,6V = 8,4V$$
$$I_{\textrm{R1}} = I_{\textrm{B}} + I_{\textrm{R2}} = I_{\textrm{B}} + 10 \cdot I_{\textrm{B}} = 110\mu A$$
$$R_1 = \frac{U_{\textrm{R1}}}{I_{\textrm{R1}}} = \frac{8,4V}{110\mu A} \approx 76,4k\Omega$$
AC519: Was passiert, wenn der Widerstand $R_1$ durch eine fehlerhafte Lötstelle an einer Seite keinen Kontakt mehr zur Schaltung hat? Welche Beschreibung trifft zu?

A: Der Kollektorstrom steigt stark an. Die Kollektorspannung erhöht sich.

B: Es fließt kein Kollektorstrom mehr. Die Kollektorspannung steigt auf die Betriebsspannung an.

C: Der Kollektorstrom wird nur durch $R_{\textrm{C}}$ begrenzt. Die Kollektorspannung sinkt auf zirka 0,1 V.

D: Es fließt Kurzschlussstrom. Der Transistor wird zerstört.

Lösungsweg

  • Kein Strom durch $R_1$ → keine Spannung über $R_2$
  • Basis liegt auf Massepotential → Transistor ist stromlos
  • Kein Spannungsabfall an $R_{\textrm{C}}$ → Kollektorpotential steigt auf Betriebsspannung
AC520: Was passiert, wenn der Widerstand $R_2$ durch eine fehlerhafte Lötstelle an einer Seite keinen Kontakt mehr zur Schaltung hat? In welcher Antwort sind beide Aussagen richtig?

A: Der Kollektorstrom wird nur durch $R_{\textrm{C}}$ begrenzt. Die Kollektorspannung sinkt auf zirka 0,1 V.

B: Es fließt Kurzschlussstrom. Der Transistor wird zerstört.

C: Der Kollektorstrom steigt stark an. Die Kollektorspannung erhöht sich.

D: Es fließt kein Kollektorstrom mehr. Die Kollektorspannung steigt auf die Betriebsspannung an.

Lösungsweg

  • $R_2$ ist stromlos → Basis ist über $R_1$ ist mit der Betriebsspannung verbunden
  • Aufgrund der Dimensionierung ist der Basisstrom nun 11-fach höher als geplant
  • Kollektorstrom wird stark ansteigen → Spannungsabfall an $R_{\textrm{C}}$ steigt stark
  • $U_{\textrm{CE}}$ sinkt auf den Sättigungswert von ca. 0,1 V

Feldeffekttransistor (FET)

1) Kurzbeschreibung: Zwei Schaltzeichen („1“ und „2“), jeweils mit einem Kreis, einem Anschluss links und zwei Anschlüssen rechts; linker Anschluss beim linken Schaltzeichen mit Pfeil nach rechts, beim rechten Schaltzeichen mit Pfeil nach links. 2) Ausführliche Beschreibung: Zwei Schaltzeichen /“1“ und „2“) bestehen aus einem Kreis mit einer vertikalen Linie links im Kreis. Von links führt ein Anschluss horizontal in den Kreis und trifft im unteren Bereich auf diese vertikale Linie. Im linken Schaltzeichen besitzt dieser Anschluss einen Pfeil in Richtung auf die Linie, im rechten Schaltzeichen zeigt der Pfeil von der Linie weg. Von der vertikalen Linie gehen im Kreis zwei parallele horizontale Linien nach rechts. Die obere endet an einem kurzen vertikalen Anschluss nach oben, die untere an einem kurzen vertikalen Anschluss nach unten.
Abbildung AS-3.7.3: Schaltbilder für Feldeffekttransistoren

  • Anderer Aufbau
  • Es besteht ein Halbleiterkanal
  • Der Stromfluss wird über ein elektrisches Feld gesteuert
  • Dadurch spannungsgesteuert
AC502: Ein Feldeffekttransistor ist ...

A: stromgesteuert.

B: leistungsgesteuert.

C: optisch gesteuert.

D: spannungsgesteuert.

AC506: Welches Bauteil wird durch das Schaltzeichen symbolisiert?

A: Diode

B: Bipolartransistor

C: Lautsprecher

D: Feldeffekttransistor

Anschlüsse des FET

  • Source Quelle für die Ladungsträger im Kanal
  • Drain Abfluss der Ladungsträger im Kanal
  • Gate steuert den Fluss der Ladungsträger im Kanal
AC513: Wie bezeichnet man die Anschlüsse des abgebildeten Transistors?

A: 1: Drain, 2: Source, 3: Gate

B: 1: Kollektor, 2: Emitter, 3: Basis

C: 1: Anode, 2: Kathode, 3: Gate

D: 1: Anode, 2: Kollektor, 3: Gate

AC512: Wie lauten die Bezeichnungen der Anschlüsse eines Feldeffekttransistors?

A: Drain, Gate, Source

B: Gate, Source, Kollektor

C: Emitter, Drain, Source

D: Emitter, Basis, Kollektor

AC514: Wie erfolgt die Steuerung des Stroms im Feldeffekttransistor (FET)?

A: Der Gatestrom steuert den Drainstrom.

B: Die Gate-Source-Spannung steuert den Gatestrom.

C: Der Gatestrom steuert den Widerstand des Kanals zwischen Source und Drain.

D: Die Gate-Source-Spannung steuert den Widerstand des Kanals zwischen Source und Drain.

Bauarten FET

  • selbstleitend: Ohne Gate-Source-Spannung ist der FET leitend
  • selbstsperrend: Ohne Gate-Source-Spannung ist der FET sperrend
  • n-Kanal-FET: Strom im Kanal wird von Elektronen getragen
  • p-Kanal-FET: Strom im Kanal wird von Löchern getragen
  • Sperrschicht-FET: Gate ist eine Diode
  • Isolierschicht-FET: Gate ist eine Kondensator-Struktur (z. B. MOSFET)

Schaltzeichen FET

1) Kurzbeschreibung: Schaltzeichen mit einem Kreis, einem Anschluss links und zwei Anschlüssen rechts sowie einem Pfeil nach rechts. 2) Ausführliche Beschreibung: Das Schaltzeichen besteht aus einem Kreis mit einer vertikalen Linie links im Kreis. Von links führt ein Anschluss von außen horizontal in den Kreis und trifft im unteren Bereich auf diese vertikale Linie. Parallel zu dieser Linie gibt es eine weitere vertikale Linie, von der drei parallele horizontale Linien nach rechts führen. Die obere endet an einem kurzen vertikalen Anschluss nach oben, die mittlere weist einen Pfeil nach rechts von der vertikalen Linie weg auf und ist im Kreis mit der unteren horizontalen Linie verbunden. Die untere horizontale Linie hat einen kurzen vertikalen Anschluss nach unten.
Abbildung AS-3.7.4: Selbstleitender p-Kanal MOSFET
1) Kurzbeschreibung: Schaltzeichen mit einem Kreis, einem Anschluss links und zwei Anschlüssen rechts sowie einem Pfeil zur Mitte. 2) Ausführliche Beschreibung: Das Schaltzeichen besteht aus einem Kreis mit einer vertikalen Linie links im Kreis. Von links führt ein Anschluss von außen horizontal in den Kreis und trifft im unteren Bereich auf diese vertikale Linie. Parallel zu dieser Linie gibt es drei kleine vertikale Striche, von denen jeweils eine parallele horizontale Linie nach rechts führt. Die obere endet an einem kurzen vertikalen Anschluss nach oben, die mittlere weist einen Pfeil nach links zur vertikalen Linie auf und ist im Kreis mit der unteren horizontalen Linie verbunden. Die untere horizontale Linie hat einen kurzen vertikalen Anschluss nach unten.
Abbildung AS-3.7.5: Selbstsperrender n-Kanal MOSFET

AC507: Welche Bezeichnungen für die Bauelemente sind richtig?

A: 1: Selbstleitender N-Kanal-Sperrschicht-FET 2: Selbstleitender P-Kanal-Sperrschicht-FET

B: 1: Selbstleitender P-Kanal-Sperrschicht-FET 2: Selbstleitender N-Kanal-Sperrschicht-FET

C: 1: Selbstsperrender N-Kanal-Sperrschicht-FET 2: Selbstsperrender P-Kanal-Sperrschicht-FET

D: 1: Selbstsperrender P-Kanal-Sperrschicht-FET 2: Selbstsperrender N-Kanal-Sperrschicht-FET

AC508: Der folgende Transistor ist ein ...

A: Selbstleitender N-Kanal-Isolierschicht-FET (MOSFET).

B: Selbstsperrender N-Kanal-Isolierschicht-FET (MOSFET).

C: Selbstleitender P-Kanal-Isolierschicht-FET (MOSFET).

D: Selbstsperrender P-Kanal-Isolierschicht-FET (MOSFET).

AC509: Welcher der folgenden Transistoren ist ein selbstsperrender N-Kanal-MOSFET?
A:
B:
C:
D:
AC510: Welcher der folgenden Transistoren ist ein selbstleitender N-Kanal-MOSFET?
A:
B:
C:
D:
AC511: Welcher der folgenden Transistoren ist ein selbstleitender P-Kanal-MOSFET?
A:
B:
C:
D:

Rechnungen

AC521: Wie groß ist die Gate-Source-Spannung in der gezeichneten Schaltung? $U_{\textrm{B}} = 44 V$; $R_1 = 10 k\Omega$; $R_2 = 1 k\Omega$; $R_3 = 2,2 k\Omega$ ...

A: 8 V

B: 4 V

C: 4,4 V

D: 0,7 V

Lösungsweg

  • gegeben: $U_{\textrm{B}} = 44 V$
  • gegeben: $R_1 = 10k\Omega$
  • gegeben: $R_2 = 1k\Omega$
  • gegeben: $R_3 = 2,2k\Omega$
  • gesucht: $U_{\textrm{GS}}$
  • Ansatz: Unbelasteter Spannungsteiler über $R_1$ und $R_2$, mit $U_{\textrm{GS}} = U_{\textrm{R2}}$
AC522: Wie groß muss $R_2$ gewählt werden, damit sich eine Spannung von 2,8 V zwischen Gate und Source einstellt? $U_{\textrm{B}}$=44 V; $R_1$=10 kOhm; $R_3$=2,2 kOhm ...

A: ca. 680 Ohm

B: ca. 1405 Ohm

C: ca. 820 Ohm

D: ca. 68 Ohm

Lösungsweg

  • gegeben: $U_{\textrm{B}} = 44 V$
  • gegeben: $R_1 = 10k\Omega$
  • gegeben: $R_3 = 2,2k\Omega$
  • gegeben: $U_{\textrm{GS}} = U_{\textrm{R2}} = 2,8 V$
  • gegeben: $U_{\textrm{B}} = U_{\textrm{R1}} + U_{\textrm{R2}}$
  • gesucht: $R_2$
AC523: Welche Verlustleistung erzeugt ein Power-MOS-FET mit $R_{\textrm{DSon}}$ = 4 \mOhm bei einem Strom von 25 A?

A: 6,25 W

B: 2,5 W

C: 0,1 W

D: 1 W

Lösungsweg

  • gegeben: $R_{\textrm{DSon}} = 4 m\Omega$
  • gegeben: $I = 25 A$
  • gesucht: $P$
$$P = I^2 \cdot R = 25^2A \cdot 4m\Omega = 2,5W$$

Freilaufdiode

  • Relais wird über einen in Serie geschalteten Bipolartransistor betrieben
  • Transistor schaltet ein → Strom fließt durch die Relaisspule
  • Transistor schaltet ab → Strom in der Spule induziert negative Spannung am Transistor
  • Kann zur Zerstörung des Transistors führen
  • Verhindern: Freilaufdiode parallel zum Relais in Sperrichtung verbauen
  • Induktionsspannung wird auf Diodenspannung begrenzt
AC524: In welcher der folgenden Schaltungen ist die Freilaufdiode richtig eingesetzt?
A:
B:
C:
D:

Integrierte Schaltkreise

  • Integrated Circuit (IC): Integrierte Schaltungen
  • Komplexe Schaltung auf einem Halbleitersubstrat
  • Erleichtern den Aufbau von elektronischen Schaltungen
AC601: Eine integrierte Schaltung ist ...

A: eine miniaturisierte, aus SMD-Bauteilen aufgebaute Schaltung.

B: eine aus einzelnen Bauteilen aufgebaute vergossene Schaltung.

C: eine komplexe Schaltung auf einem Halbleitersubstrat.

D: die Zusammenschaltung einzelner Baugruppen zu einem elektronischen Gerät.

Monolithic Microwave Integrated Circuit (MMIC)

  • Breitbandiger Verstärker mit wenigen Bauteilen
  • Typischerweise 50Ω Ein- und Ausgangsimpedanz
  • Vereint aktive und passive Bauelemente
AC602: Welche Bauteile sind in einem Monolithic Microwave Integrated Circuit (MMIC) enthalten?

A: Ein MMIC enthält nur passive Bauteile auf einem Halbleiter-Substrat.

B: Ein MMIC enthält alle aktiven und passiven Bauteile auf einer Leiterplatte.

C: Ein MMIC enthält nur aktive Bauteile auf einem Halbleiter-Substrat.

D: Ein MMIC enthält alle aktiven und passiven Bauteile auf einem Halbleiter-Substrat.

AC603: Welchen Vorteil hat ein Monolithic Microwave Integrated Circuit (MMIC) gegenüber einem diskreten Transistorverstärker?

A: Ein MMIC bietet breitbandig eine hohe Verstärkung mit weniger Bauteilen.

B: Ein MMIC bietet einstellbare Eingangs- und Ausgangsimpedanz.

C: Ein MMIC bietet einen hohen Eingangswiderstand und einen niedrigen Ausgangswiderstand.

D: Ein MMIC bietet schmalbandig eine hohe Verstärkung in einem Bauteil.

AC604: Was ist typisch für einen Monolithic Microwave Integrated Circuit (MMIC)?

A: Sie sind nur im Mikrowellenbereich einsetzbar.

B: Die Verstärkung ist bereits ab 0 Hz konstant.

C: Ein- und Ausgangsimpedanz entsprechen üblichen Leitungsimpedanzen (z. B. 50 Ohm).

D: Der Verstärkungsbereich ist schmalbandig.

MMIC Beschaltung

1) Kurzbeschreibung: Schaltplan in rechteckiger Leitungsführung mit einem MMIC, mehreren Kondensatoren, einer Spule und einem Widerstand. 2) Ausführliche Beschreibung: Der Schaltplan enthält einen rechteckigen Schaltkreis mit zwei horizontalen Leitern (in der Mitte und oben). Der mittlere besitzt Anschlusspunkte links („RF_IN“) und rechts („RF_OUT“). Der linke Anschlusspunkt ist über einen Kondensator C_1 mit dem Eingang 1 eines MMIC verbunden. Ausgang 2 liegt an Masse. Ausgang 3 führt über einen Kondensator C_3 zum rechten Anschlusspunkt. Ausgang 4 ist mit einem Verzweigungspunkt verbunden, der einerseits an Masse liegt und andererseits über einen Kondensator C_2 und eine Spule zu einem Anschlusspunkt („U_CC“) führt. Zwischen dem rechten Ende von C_2 und Ausgang 3 des MMIC liegt ein Widerstand R_BIAS. In der Abbildung ist ein weiterer Massepunkt eingezeichnet. Zwischen dem Ausgang 3 und diesem Massepunkt gibt es einen vertikalen Pfeil nach unten mit der Beschriftung „U_D = 4 V“.
Abbildung AS-3.8.1: MMIC-Schaltung

AF425: Der optimale Arbeitspunkt des dargestellten MMIC ist mit 4 V und 10 mA angegeben. Die Betriebsspannung beträgt 13,5 V. Berechnen Sie den Vorwiderstand ($R_\text{BIAS}$).

A: 400 Ohm

B: 95 Ohm

C: 950 Ohm

D: 1350 Ohm

Lösungsweg

  • gegeben: $U_{\textrm{D}} = 4 V$
  • gegeben: $U_{\textrm{CC}} = 13,5 V$
  • gegeben: $I_{\textrm{D}} = 10 mA$
  • gesucht: $R_{\textrm{BIAS}}$
$$R_{\textrm{BIAS}} = \frac{U_{\textrm{CC}} - U_{\textrm{D}}}{I_{\textrm{D}}} = \frac{13,5V -4V}{10mA} = 950\Omega$$
AF426: Berechnen Sie $R_\text{BIAS}$ für die dargestellte MMIC-Schaltung und wählen Sie den nächsten Normwert. $U_\text{CC}$ = 13,8 V; $U_\text{D}$ = 4 V; $I_\text{D}$ = 15 mA

A: 820 Ohm

B: 680 Ohm

C: 270 Ohm

D: 560 Ohm

Lösungsweg

  • gegeben: $U_{\textrm{D}} = 4 V$
  • gegeben: $U_{\textrm{CC}} = 13,8 V$
  • gegeben: $I_{\textrm{D}} = 15 mA$
  • gesucht: $R_{\textrm{BIAS}}$
$$R_{\textrm{BIAS}} = \frac{U_{\textrm{CC}} - U_{\textrm{D}}}{I_{\textrm{D}}} = \frac{13,8V -4V}{15mA} = 653,3\Omega \rightarrow 680\Omega$$
AF427: Wieviel Wärmeleistung wird im MMIC in Wärme umgesetzt, wenn die Betriebsspannung 9 V beträgt und $R_\text{BIAS}$ einen Wert von 470 Ohm hat?

A: 52 mW

B: 47 mW

C: 43 mW

D: 90 mW

Lösungsweg

  • gegeben: $U = 9 V$
  • gegeben: $R_{\textrm{BIAS}} = 470\Omega$
  • gegeben: $U_{\textrm{D}} = 4 V$
  • gesucht: $P$
  • Ansatz: Strom durch $R_{\textrm{BIAS}}$ ist überall gleich, weil kein anderer ohmschmer Verbraucher in der Schaltung vorhanden ist
$$I_{\textrm{D}} = \frac{U_{\textrm{BIAS}}}{R_{\textrm{BIAS}}} = \frac{U-U_{\textrm{D}}}{R_{\textrm{BIAS}}} = \frac{9V-4V}{470\Omega} = 10,64mA$$
$$P = U_{\textrm{D}} \cdot I_{\textrm{D}} = 4V \cdot 10,64mA \approx 43mW$$

Fragen?

Links zu diesem Foliensatz