Digitale Signalverarbeitung

Navigationshilfe

Diese Navigationshilfe zeigt die ersten Schritte zur Verwendung der Präsentation. Sie kann mit ⟶ (Pfeiltaste rechts) übersprungen werden.

Navigation

Zwischen den Folien und Abschnitten kann man mittels der Pfeiltasten hin- und herspringen, dazu kann man auch die Pfeiltasten am Computer nutzen.

Navigationspfeile für die Präsentation

Weitere Funktionen

Mit ein paar Tastenkürzeln können weitere Funktionen aufgerufen werden. Die wichtigsten sind:

F1
Help / Hilfe
o
Overview / Übersicht aller Folien
s
Speaker View / Referentenansicht
f
Full Screen / Vollbildmodus
b
Break, Black, Pause / Ausblenden der Präsentation
Alt-Click
In die Folie hin- oder herauszoomen

Übersicht

Die Präsentation ist zweidimensional aufgebaut. Dadurch sind in Spalten die einzelnen Abschnitte eines Kapitels und in den Reihen die Folien zu den Abschnitten.

Tippt man ein „o“ ein, bekommt man eine Übersicht über alle Folien des jeweiligen Kapitels. Das hilft sich zunächst einen Überblick zu verschaffen oder sich zu orientieren, wenn man das Gefühlt hat sich „verlaufen“ zu haben. Die Navigation erfolgt über die Pfeiltasten.

Referentenansicht

Referentenansicht

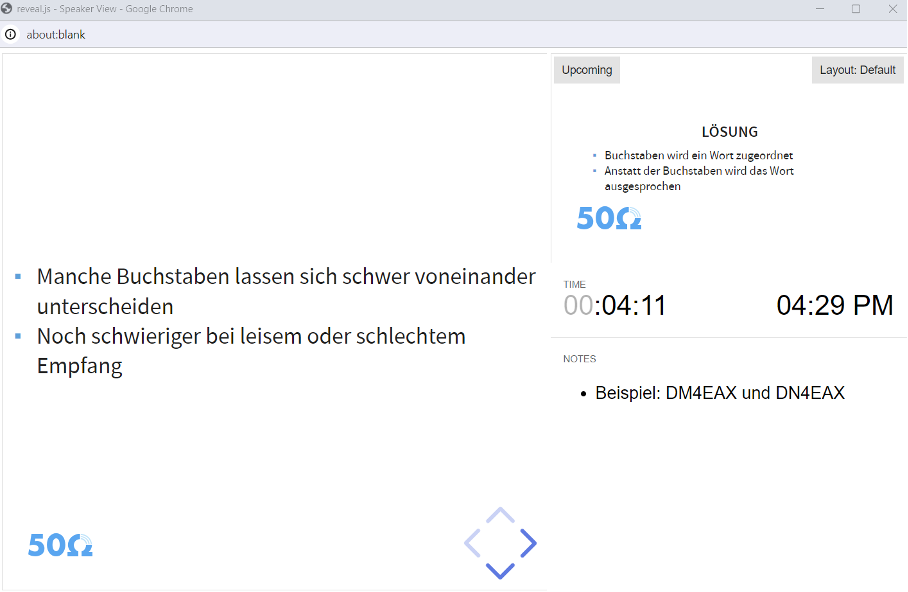
Tippt man ein „s“ ein, bekommt man ein neues Fenster, die Referentenansicht.

Indem man „Layout“ auswählt, kann man zwischen verschieden Anordnungen der Elemente auswählen.

Praxistipps zur Referentenansicht

  • Wenn man mit einem Projektor arbeitet, stellt man im Betriebssystem die Nutzung von 2 Monitoren ein: Die Referentenansicht wird dann zum Beispiel auf dem Laptop angezeigt, während die Teilnehmer die Präsentation angezeigt bekommen.
  • Bei einer Online-Präsentation, wie beispielsweise auf TREFF.darc.de präsentiert man den Browser-Tab und navigiert im „Speaker View“ Fenster.
  • Die Referentenansicht bezieht sich immer auf ein Kapitel. Am Ende des Kapitels muss sie geschlossen werden, um im neuen Kapitel eine neue Referentenansicht zu öffnen.
  • Um mit dem Mauszeiger etwas zu markieren oder den Zoom zu verwenden, muss mit der Maus auf den Bildschirm mit der Präsentation gewechselt werden.

Vollbild

Tippt man ein „f“ ein, wird die aktuelle Folie im Vollbild angezeigt. Mit „Esc“ kann man diesen wieder verlassen.

Das ist insbesondere für den Bildschirm mit der Präsentation für das Publikum praktisch.

Ausblenden

Tippt man ein „b“ ein, wird die Präsentation ausgeblendet.

Sie kann wie folgt wieder eingeblendet werden:

  • Durch klicken in das Fenster.
  • Durch nochmaliges Drücken von „b“.
  • Durch klicken der Schaltfläche „Resume presentation:
Schaltfläche für Resume Presentation

Zoom

Bei gedrückter Alt-Taste und einem Mausklick in der Präsentation wird in diesen Teil hineingezoomt. Das ist praktisch, um Details von Schaltungen hervorzuheben. Durch einen nochmaligen Mausklick zusammen mit Alt wird wieder herausgezoomt.

Das Zoomen funktioniert nur im ausgewählten Fenster. Die Referentenansicht ist hier nicht mit dem Präsenationsansicht gesynct.

Sampling und Quantisierung

Sampling: Von analog zu digital

  • Analoge Signale werden mittels Sampling in digitale Werte umgewandelt
  • Abtastung erfolgt in definierten Zeitintervallen – nur Momentanzustände werden gemessen
  • Analoge Signale sind zeitkontinuierlich, da sie keine kleinste zeitliche Auflösung besitzen
  • Digitale Samples sind zeitdiskret, da ein festes Abtastintervall existiert

Hier gibt es die Möglichkeit das Ganze nochmal auszuprobieren. Ein zeitkontinuierliches Sinus-Signal wird von einem AD-Umsetzer digitalisiert und anschließend wieder von einem DA-Umsetzer in ein analoges Signal gewandelt. An den Reglern kann man die Zeitquantisierung und die Wertquantisierung der AD/DA-Umsetzer einstellen.


Zeit-Quantisierung:
1024
Samples/s.
Wert-Quantisierung:
16
bits

Wertkontinuität vs. Wertdiskretheit

  • Analoge Signale können beliebige Spannungswerte annehmen – sie sind wertkontinuierlich
  • Bei der Digitalisierung gibt es nur begrenzte Abstufungen (z. B. -128 bis +127) – Samples sind wertdiskret
  • Zwischen zwei Spannungsstufen muss der A/D-Umsetzer eine Entscheidung treffen (Quantisierung)

Praktisches Beispiel: Dimmer vs. Stufenschalter

  • Ein analoger Dimmer erlaubt feine, stufenlose Helligkeitseinstellungen
  • Ein Stufenschalter (z. B. 5 Stufen) ermöglicht nur feste Helligkeitswerte – Zwischenstufen sind nicht möglich
  • Quantisierung: Auswahl der nächstpassenden Stufe, um den analogen Wert abzubilden
AF601: Welche der folgenden Abbildungen symbolisiert ein zeitkontinuierliches und wertkontinuierliches Signal am besten?
A:
B:
C:
D:
AF603: Welche der folgenden Abbildungen symbolisiert ein zeitdiskretes und wertkontinuierliches Signal am besten?
A:
B:
C:
D:
AF602: Welche der folgenden Abbildungen symbolisiert ein zeitkontinuierliches und wertdiskretes Signal am besten?
A:
B:
C:
D:
AF604: Welche der folgenden Abbildungen symbolisiert ein zeitdiskretes und wertdiskretes Signal am besten?
A:
B:
C:
D:

Sampling

  • Der Prozess, ein analoges, zeitkontinuierliches Signal mittels A/D-Umsetzung in ein digitales Signal zu überführen
  • Das digitale Signal besteht aus einzelnen, zeitdiskreten Samples
AF606: Wie wird die Umwandlung eines zeitkontinuierlichen in ein zeitdiskretes Signal bezeichnet?

A: Codierung

B: Quantisierung

C: Sampling

D: Zeitmultiplexing

Samplingrate

  • Geschwindigkeit, mit der ein A/D-Umsetzer Abtastungen vornimmt
  • Definiert als Anzahl der Samples pro Zeiteinheit (z. B. pro Sekunde)
  • Einheit: Samples/s (z. B. 44,100 Samples/s bei CDs, oft als 44,1 ksps angegeben)
AF615: Wie ist die Abtastrate (Samplingrate) eines A/D-Umsetzers definiert?

A: Abtastungen mal Zeit

B: Abtastungen mal Samples

C: Abtastungen je Hertz

D: Abtastungen je Zeiteinheit

Abtasttheorem

Der Prozess des Samplings

  • Analoge Signale werden in diskrete Samples umgewandelt
  • Sampling: Abtastung eines kontinuierlichen Signals in festgelegten Zeitabständen
  • Vergleichbar mit einer Kamera, die in regelmäßigen Intervallen Bilder aufnimmt

Sampling – Das Kamerabeispiel

  • Eine Kamera nimmt z. B. 24 Bilder pro Sekunde auf
  • Zwischen den Bildern können schnelle Bewegungen auftreten, die nicht erfasst werden
  • Wie bei der Kamera kann ein plötzliches Ereignis (z. B. eine Fliege) zwischen zwei Aufnahmen verloren gehen
  • Dadurch entsteht ein Verlust an zeitlicher Information

Informationsverlust und Rekonstruktionsgrenze

  • Zwischen den Samples können schnelle Signaländerungen unentdeckt bleiben
  • Für eine fehlerfreie Rekonstruktion muss vor und nach jedem Signalwechsel ein Sample vorliegen
  • Ist dies nicht der Fall, gehen Details verloren – Aliasing tritt auf

Das Nyquist-Shannon-Abtasttheorem

  • Für ein Signal mit maximaler Frequenz $f_{max}$ muss die Abtastrate $\gt 2 \cdot f_{max}$ betragen
  • Nur so können alle Signalwechsel korrekt erfasst und rekonstruiert werden
  • Wird diese Grenze unterschritten, entstehen Alias-Effekte
AF617: Unter dem Alias-Effekt werden Fehler verstanden, die ...

A: beim Senden mit mehrelementigen Richtantennen auftreten, deren Elementabstand größer als die halbe Wellenlänge ist.

B: bei Mehrwegeausbreitung mit Laufzeitunterschieden auftreten, die höher als die halbe Dauer einer Schwingung des Trägers sind.

C: bei der Abtastung von Frequenzanteilen auftreten, die höher als die halbe Abtastfrequenz sind.

D: beim Empfang eines Signals auftreten, von dessen Spektrum mehr als die Hälfte gestört ist.

Praktisches Beispiel: CD-Player

  • CD-Player arbeiten typischerweise mit 44,1 ksps (44.100 Samples pro Sekunde)
  • Daraus folgt: Frequenzen bis ca. 22 kHz können korrekt abgebildet werden
  • Dies entspricht dem HiFi-Frequenzbereich guter Stereoanlagen
  • Merke: Die Abtastfrequenz sollte stets knapp über dem Doppelten der maximal zu verarbeitenden Frequenz liegen
AF616: Welche Aussage trifft auf das Abtasttheorem zu? Das Theorem ...

A: bestimmt die maximale Bandbreite, die durch eine Übertragung mit einer bestimmten Datenübertragungsrate theoretisch belegt werden kann.

B: bestimmt die für eine fehlerfreie Rekonstruktion eines Signals theoretisch notwendige minimale Abtastrate.

C: besagt, dass unabhängig von der Art der vorherrschenden Störungen eines Übertragungskanals theoretisch eine unbegrenzte Datenübertragungsrate erzielt werden kann.

D: besagt, dass theoretisch eine unendliche Abtastrate erforderlich ist, um ein bandbegrenztes Signal fehlerfrei zu rekonstruieren.

AF618: Ein analoges Signal mit einer Bandbreite von $f_{\textrm{max}}$ soll digital verarbeitet werden. Welche der folgenden Abtastraten ist die kleinste, die Alias-Effekte vermeidet?

A: knapp über $f_{\textrm{max}}$

B: knapp unter $\dfrac{f_{\mathrm{max}}}{2}$

C: knapp über $2 \cdot f_{\textrm{max}}$

D: knapp unter $f_{\textrm{max}}$

AF619: Ein analoges Sprachsignal mit 4 kHz Bandbreite soll digital verarbeitet werden. Welche der folgenden Abtastraten ist die kleinste, die Alias-Effekte vermeidet?

A: 2400 Samples/s

B: 4000 Samples/s

C: 4800 Samples/s

D: 9600 Samples/s

Quantisierung

Quantisierung in der A/D-Umsetzung

  • Zeitkontinuierliche Signale werden durch A/D-Umsetzung in digitale Samples überführt
  • Bei der Quantisierung werden kontinuierliche analoge Werte in feste Stufen (wertdiskret) abgebildet
  • Ein analoges, wertkontinuierliches Signal wird somit in ein gestuftes, wertdiskretes Signal transformiert
AF605: Wie wird die Umwandlung eines wertkontinuierlichen in ein wertdiskretes Signal bezeichnet?

A: Raummultiplexing

B: Quantisierung

C: Codierung

D: Sampling

Analog-Digital-Umsetzer (ADC)

Funktion des A/D-Umsetzers

  • Wandelt analoge Eingangssignale in digitale Samples um
  • Essentiell für die Digitalisierung und Weiterverarbeitung von Signalen

Aliasing und Antialiasing

  • Abtasttheorem: Für fehlerfreie Rekonstruktion muss die Abtastrate $\gt 2 \cdot f_{max}$ betragen
  • Signale oberhalb der maximal verarbeitbaren Frequenz können als fehlerhafte Aliases erscheinen
  • Antialiasing-Filter (Tiefpass- oder Bandpassfilter) unterdrücken unerwünschte hohe Frequenzen
  • Schützen den A/D-Umsetzer vor fehlerhaften Aliasing-Effekten
AF620: Welche Funktionen haben die einzelnen Blöcke im dargestellten Blockschaltbild eines digitalen Direktempfängers?

A: 1: Abtastratengenerator, 2: Antialiasing-Filter, 3: Analog-Digital-Umsetzer

B: 1: Analog-Digital-Umsetzer, 2: Antialiasing-Filter, 3: Abtastratengenerator

C: 1: Antialiasing-Filter, 2: Abtastratengenerator, 3: Analog-Digital-Umsetzer

D: 1: Analog-Digital-Umsetzer, 2: Abtastratengenerator, 3: Antialiasing-Filter

Taktgenerator (Abtastratengenerator)

  • Erzeugt den exakten zeitlichen Takt für die Abtastung
  • Bestimmt, wie oft pro Sekunde ein Sample erfasst wird
  • Kann fest eingestellt oder durch Steuerung (z. B. Mikrocontroller) geregelt werden

Quantisierung und Quantisierungsfehler

  • Bei der A/D-Umsetzung werden analoge Amplitudenwerte in feste Stufen abgebildet
  • Dies führt zu einer wertdiskreten Darstellung des ursprünglich kontinuierlichen Signals
  • Quantisierungsfehler entstehen, da nicht alle Zwischenwerte exakt erfasst werden können
AF607: Warum kommt es in einem A/D-Umsetzer zu Quantisierungsfehlern?

A: Es können nur ganzzahlige Frequenzen verwendet werden.

B: Es können nur Werte zwischen 0 und 1 genutzt werden.

C: Die Bandbreite des Eingangssignals ist begrenzt.

D: Es steht nur eine begrenzte Anzahl diskreter Werte zur Verfügung.

Auflösung des A/D-Umsetzers

  • Anzahl der möglichen digital darstellbaren Stufen
  • Wird in Bit angegeben (z. B. 8 Bit = 256 Stufen, 16 Bit = 65.536 Stufen)
  • Häufig wird die Hälfte der Werte für den positiven und die andere Hälfte für den negativen Bereich verwendet
AF608: Wie viele Bereiche von Eingangswerten, z. B. Spannungen, kann ein A/D-Umsetzer mit 8 Bit Auflösung maximal trennen?

A: 64

B: 256

C: 1024

D: 8

Jitter: Timing-Instabilitäten

  • Jitter beschreibt kleine, zufällige Schwankungen in den Abtastzeitpunkten
  • Ein instabiler Abtastratengenerator führt zu zusätzlichen Rauscheffekten im digitalen Signal
  • Hoher technischer Aufwand ist nötig, um einen präzisen Takt zu gewährleisten
AF621: Bei einer Abtastung mit einem A/D-Umsetzer mit 24 Bit Auflösung wird ein Oszillator mit starkem Taktzittern (Jitter) eingesetzt. Welche Auswirkung wird das Zittern haben?

A: Das Abschirmblech des A/D-Umsetzers wird durch Vibration störende Geräusche erzeugen.

B: Es entsteht zusätzliches Rauschen im Abtastergebnis.

C: Aufgrund der großen Auflösung bleibt die Schwankung ohne Auswirkung.

D: Das Abtastergebnis wird verbessert (Dithering).

Digital-Analog-Umsetzer (DAC)

D/A-Umsetzer: Vom Digitalen zum Analogen

  • Der D/A-Umsetzer wandelt einen digitalen Datenstrom (Samples) in ein analoges Signal um
  • Genau wie der A/D-Umsetzer hat er eine begrenzte Auflösung (in Bit)
  • Dadurch gibt es eine endliche Anzahl an analogen Signalwerten
AF609: Wie viele verschiedene Ausgangswerte, z. B. Spannungen, kann ein idealer D/A-Umsetzer mit 10 Bit Auflösung erzeugen?

A: 10

B: 100

C: 1024

D: 256

Auflösung und Spannungsbereich

  • Die Anzahl der möglichen Stufen wird durch die Bit-Auflösung bestimmt
  • Beispiel: 4 Bit → 16 mögliche Stufen
  • Ein D/A-Umsetzer arbeitet in einem festen Spannungsbereich (z. B. 0 bis 1 V)
  • Bei einem linear arbeitenden D/A-Umsetzer verteilt sich der Spannungsbereich gleichmäßig auf die Stufen

Schrittweite (Quantisierungsintervall)

  • Die Schrittweite berechnet sich aus dem Spannungsbereich geteilt durch die Anzahl der Stufen
  • Beispiel: Bei 16 Stufen und einem Bereich von 0 bis 1 V ergibt sich eine Schrittweite von ca. 6,25 mV
AF611: Wie groß ist die Schrittweite zwischen den Spannungsstufen eines linear arbeitenden D/A-Umsetzers mit 10 Bit Auflösung und einem Wertebereich von 0 bis 1 V?

A: ca. 1 V

B: ca. 1 mV

C: ca. 10 mV

D: ca. 0,1 V

AF610: Wie groß ist die Schrittweite zwischen den Spannungsstufen eines linear arbeitenden D/A-Umsetzers mit 8 Bit Auflösung und einem Wertebereich von 0 bis 1 V?

A: ca. 1 mV

B: ca. 2 mV

C: ca. 4 mV

D: ca. 8 mV

Anwendung von ADC und DAC

A/D- und D/A-Umsetzer in SDR-Systemen

  • In SDR-Empfängern und Transceivern wandeln A/D-Umsetzer analoge Eingangssignale in digitale Daten um
  • Die digitalen Daten werden verarbeitet und mittels D/A-Umsetzer wieder in analoge Signale umgewandelt

Nutzung des Wertebereichs

  • Wird der volle Wertebereich nicht ausgenutzt, wird das Signal nur auf einen kleineren digitalen Bereich abgebildet
  • Überschreitet das Eingangssignal den maximalen Bereich, kann der A/D-/D/A-Umsetzer nur bis zur maximalen Spannung korrekt abbilden
  • Überschüssige Werte werden als Maximalwert (Clipping) dargestellt, was zu abgeschnittenen Signalanteilen führt

Einfluss der Auflösung

  • Eine höhere Auflösung ermöglicht eine feinere Abbildung der Signalamplituden
  • Eine niedrigere Auflösung führt zu einer gestuften, weniger genauen Rekonstruktion des Signals
AF613: Eine Sinusschwingung mit einem Spitzenwert von 1,5 V wird in einen A/D-Umsetzer eingegeben, dessen Ausgang direkt mit einem D/A-Umsetzer verbunden ist. Beide Umsetzer arbeiten linear mit einer Auflösung von 12 Bit und einem Wertebereich von -2 V bis 2 V. Welches Signal ist am Ausgang des D/A-Umsetzers zu erwarten?
A:
B:
C:
D:
AF612: Eine Sinusschwingung mit einem Spitzenwert von 1,5 V wird in einen A/D-Umsetzer eingegeben, dessen Ausgang direkt mit einem D/A-Umsetzer verbunden ist. Beide Umsetzer arbeiten linear mit einer Auflösung von 4 Bit und einem Wertebereich von -2 V bis 2 V. Welches Signal ist am Ausgang des D/A-Umsetzers zu erwarten?
A:
B:
C:
D:
AF614: Eine Sinusschwingung mit einem Spitzenwert von 1,5 V wird in einen A/D-Umsetzer eingegeben, dessen Ausgang direkt mit einem D/A-Umsetzer verbunden ist. Beide Umsetzer arbeiten linear mit einer Auflösung von 12 Bit und einem Wertebereich von -1 V bis 1 V. Welches Signal ist am Ausgang des D/A-Umsetzers zu erwarten?
A:
B:
C:
D:

Anti-Alias-Filter

Antialiasingfilter vor dem A/D-Umsetzer

  • Vor dem A/D-Umsetzer wird ein Filter eingesetzt, um Signalanteile höherer Frequenzen zu unterdrücken
  • Solche Filter werden als Antialiasingfilter bezeichnet
  • Ziel: Vermeidung von Alias-Effekten durch Abschwächung unerwünschter Frequenzen

Filtertypen und Anforderungen

  • Tiefpass- oder Bandpassfilter können eingesetzt werden
  • Das Filter muss Signalanteile oberhalb der halben Sampling-Frequenz wirksam dämpfen
  • Voraussetzung: Die Abtastfrequenz muss mehr als das Doppelte der zu erfassenden Signalfrequenz betragen
AF622: Welcher Filtertyp ist geeignet, um Alias-Effekte zu vermeiden, und wo ist das Filter zu platzieren?

A: Hochpassfilter vor dem A/D-Umsetzer

B: Hochpassfilter nach dem D/A-Umsetzer

C: Tiefpassfilter nach dem D/A-Umsetzer

D: Tiefpassfilter vor dem A/D-Umsetzer

AF623: Sie wollen ein Sprachsignal mit einer Abtastrate von $f_{\textrm{A}}$ = 8000 Samples je Sekunde digitalisieren. Vor dem A/D-Umsetzer soll ein Anti-Alias-Filter eingesetzt werden. Welcher Amplitudengang ist für das Filter am besten geeignet?
A:
B:
C:
D:

Rekonstruktionsfilter

Rekonstruktion durch den D/A-Umsetzer

  • Wandelt digitale Samples zurück in analoge Spannungsstufen
  • Samples werden in festgelegten zeitlichen Abständen wieder ausgegeben
  • Vorgang: Rekonstruktion des ursprünglichen Signals

Stufenförmiges Signal und Filterung

  • Zeitdiskrete Abtastung führt zu einem stufenförmigen Signal
  • Unerwünschte höhere Frequenzen (Artefakte) können auftreten
  • Einsatz eines Rekonstruktionsfilters (Tiefpass- oder Bandpassfilter)
  • Filter unterdrückt alle Signalanteile oberhalb der halben Abtastrate
AF624: Welcher Filtertyp ist als Rekonstruktionsfilter geeignet und wo ist das Filter zu platzieren?

A: Tiefpassfilter vor dem A/D-Umsetzer

B: Tiefpassfilter nach dem D/A-Umsetzer

C: Hochpassfilter vor dem A/D-Umsetzer

D: Hochpassfilter nach dem D/A-Umsetzer

AF625: Sie wollen ein Sprachsignal mit einer Abtastrate von $f_{\textrm{A}}$ = 8000 Samples je Sekunde rekonstruieren. Nach dem D/A-Umsetzer soll ein Rekonstruktionsfilter eingesetzt werden. Welcher Amplitudengang ist für das Filter am besten geeignet?
A:
B:
C:
D:

Fourier-Transformation

Fourier-Transformation und Signalzerlegung

  • Signale können sowohl im Zeit- als auch im Frequenzbereich dargestellt werden
  • Im Zeitbereich: X-Achse → Zeit, Y-Achse → Spannung oder Leistung
  • Im Frequenzbereich: X-Achse → Frequenz, Y-Achse → Amplitude oder Leistung

Zerlegung von Signalen

  • Jedes Signal lässt sich als Überlagerung von Sinusschwingungen darstellen
  • Jede Sinusschwingung hat eine bestimmte Amplitude und Phase
  • Dieses Prinzip ermöglicht es, komplexe Signale in ihre Bestandteile zu zerlegen

Fourier-Transformation

  • Mathematisch komplexes Verfahren, das ein zeitliches Signal analysiert
  • Zeigt an, welche Sinus-Schwingungen (Frequenzen) im Signal enthalten sind
  • Das Ergebnis wird als Frequenzspektrum dargestellt (X-Achse: Frequenz, Y-Achse: Amplitude/Leistung)

Fast Fourier Transformation (FFT)

  • Effiziente Berechnung der diskreten Fourier-Transformation (DFT)
  • Reduziert den Rechenaufwand erheblich
  • Weit verbreitet in Soft- und Hardware zur Signalverarbeitung

Beispiel: Rechtecksignal und Oberschwingungen

  • Rechtecksignale enthalten neben der Grundschwingung auch zahlreiche Oberschwingungen
  • Diese Oberschwingungen (ungerade Vielfache der Grundfrequenz) nehmen ab, sind aber deutlich sichtbar
  • Ohne Tiefpassfilter würden diese hohen Frequenzanteile stören
AF630: Wozu dient die diskrete Fouriertransformation mittels FFT? Es ist eine schnelle mathematische Methode zur Umwandlung ...

A: eines diskreten Widerstandswertes in eine Impedanz.

B: eines Widerstandswertes in einen diskreten Leitwert.

C: eines zeitdiskreten Signals in ein analoges Signal.

D: eines zeitdiskreten Signals in ein Frequenzspektrum.

AB404: Welches Frequenzspektrum passt zu folgendem sinusförmigen Signal?
A:
B:
C:
D:
AB405: Welches Frequenzspektrum passt zu folgendem periodischen Signal?
A:
B:
C:
D:
AB406: Welches Signal passt zu folgendem Frequenzspektrum?
A:
B:
C:
D:
AB407: Welches Signal passt zu folgendem Frequenzspektrum?
A:
B:
C:
D:

Digitale Filter

Digitale Signalverarbeitung: Filter

  • Digitale Informationen können nahezu beliebig bearbeitet werden
  • Eingangssamples werden mittels mathematischer Funktionen in Ausgangssamples umgerechnet
  • Filteroperationen können digital implementiert werden (z. B. Tief-, Band- oder Hochpass)

FIR-Filter (Finite Impulse Response)

  • „Finite“ = Es werden nur eine begrenzte Anzahl von Eingangssamples für jedes Ausgangssample genutzt
  • Keine Rückkopplung; Berechnung basiert ausschließlich auf aktuellen und vergangenen Samples

IIR-Filter (Infinite Impulse Response)

  • „Infinite“ = Berechnung eines Ausgangssamples bezieht sich auf alle bisherigen Eingangssamples
  • Einsatz von Rückkopplung führt zu einem theoretisch unendlichen Impulsverhalten
AF631: Welche der folgenden Aussagen zu digitalen Filtern ist richtig? Digitale Filter können ...

A: nicht in Hardware realisiert werden.

B: ohne Latenz realisiert werden.

C: nicht in Software realisiert werden.

D: als FIR- oder IIR-Filter realisiert werden.

I/Q-Verfahren

QAM und I/Q-Verfahren

  • Digitale Modulationstechnik, die zwei Träger derselben Frequenz verwendet
  • Einer der Träger ist um 90° phasenverschoben
  • Erzeugt ein Signal, das sich in Amplitude und Phase ändert

Erzeugung von QAM

  • Zwei Träger:
  • Einer wird mit dem I-Signal (In-Phase) moduliert
  • Der andere, um 90° verschoben, mit dem Q-Signal (Quadrature)
Das Ganze lässt sich leicht mathematisch beschreiben. Für die Summe eines Sinus-Trägers mit einem anderen um 90° phasenverschoben Sinus-Träger gilt folgender Zusammenhang:

$ I(t)\cdot \sin(\omega t) + Q(t)\cdot \sin(\omega t + 90°)=A \cdot \sin(\omega t+\phi) $


Es entsteht ein, also ein neues Sinussignal mit einer Amplitude von $A=\sqrt{I(t)^2 + Q(t)^2}$ und einer Phasenverschiebung von $ \phi = \arctan\left(\frac{Q(t)}{I(t)}\right)$

$I(t)=$
50%

$Q(t)=$
50%


$A=$
0
und $\phi=$
0

Man kann das auch als Konstellationsdiagramm betrachten:
AE404: Wie wird Quadraturamplitudenmodulation (QAM) üblicherweise erzeugt? Durch ...

A: Änderung der Amplituden und Addition zweier um 90° phasenverschobener Träger

B: separate Änderung der Amplitude des elektrischen und magnetischen Feldwellenanteils

C: richtungsabhängige Änderung der Frequenz (bzw. richtungsinvariante Änderung der Amplitude)

D: nichtlineare Änderung der Amplitude (Quadratfunktion bzw. Quadratwurzel)

AF632: Wie groß muss die Phasenverschiebung $\varphi$ in der dargestellten Modulatorschaltung sein, damit eine korrekte Quadraturmodulation vorliegt?

A: 45°

B: 90°

C: 180°

D: 0°

I/Q-Verfahren – Senderseite

  • Der digitale Datenstrom wird in zwei Teile aufgeteilt: I und Q
  • Zwei D/A-Umsetzer wandeln die digitalen I- und Q-Werte in analoge Signale um
  • Diese modulieren die beiden phasenverschobenen Träger, die anschließend kombiniert werden

I/Q-Verfahren – Empfängerseite

  • Das empfangene Signal wird mit einem 0°-Träger gemischt, um das I-Signal zu extrahieren
  • Gleichzeitig erfolgt eine Mischung mit einem um 90° phasenverschobenen Träger, um das Q-Signal zu erhalten
  • Beide Signale werden A/D-umgesetzt und bilden so den digitalen I/Q-Datenstrom
AF633: Was bildet der I- bzw. der Q-Anteil eines I/Q-Signals ab?

A: Den Wechselstrom (I) in Abhängigkeit der Güte (Q) eines Schwingkreises bei seiner Resonanzfrequenz

B: Den Stromanteil (I) und den Blindleistungsanteil (Q) eines Signals

C: Die erste (I) bzw. die vierte (Q) Harmonische in Bezug auf ein normiertes Rechtecksignal

D: Die phasengleichen (I) bzw. die um 90° phasenverschobenen (Q) Anteile eines Signals in Bezug auf eine Referenzschwingung

Abbildung des Frequenzbereichs

  • Der I/Q-Datenstrom bildet den Frequenzbereich um eine Mittenfrequenz ab
  • Beispiel:
  • 435 MHz-Träger
  • Abtastrate von 10 Mio. Samples/s → Bandbreite = 10 MHz (±5 MHz um die Mittenfrequenz)
  • Abgedeckter Bereich: ca. 430 bis 440 MHz
AF634: Welchen Frequenzbereich (z. B. in Bezug auf eine Mitten- oder Trägerfrequenz) kann ein digitaler Datenstrom entsprechend dem Abtasttheorem maximal eindeutig abbilden, der aus einem I- und einem Q-Anteil mit einer Abtastrate von jeweils 48000 Samples pro Sekunde besteht? Den Bereich zwischen ...

A: 0 Hz und 96 kHz.

B: -24 kHz und +24 kHz.

C: 0 Hz und 6 kHz.

D: -48 kHz und +48 kHz.

Abhängigkeit der Bandbreite von der Abtastrate

  • Die abgedeckte Bandbreite in Hz entspricht der Abtastrate in Samples pro Sekunde
AF635: Welchen Frequenzbereich (z. B. in Bezug auf eine Mitten- oder Trägerfrequenz) kann ein digitaler Datenstrom entsprechend dem Abtasttheorem maximal eindeutig abbilden, der aus einem I- und einem Q-Anteil mit einer Abtastrate von jeweils 96000 Samples pro Sekunde besteht? Den Bereich zwischen ...

A: -48 kHz und +48 kHz.

B: 0 Hz und 192 kHz.

C: -24 kHz und +24 kHz.

D: 0 Hz und 9,6 kHz.

AF636: Welchen Frequenzbereich (z. B. in Bezug auf eine Mitten- oder Trägerfrequenz) kann ein digitaler Datenstrom entsprechend dem Abtasttheorem maximal eindeutig abbilden, der aus einem I- und einem Q-Anteil mit einer Abtastrate von jeweils 10 Millionen Samples pro Sekunde besteht? Den Bereich zwischen ...

A: -5 MHz und +5 MHz.

B: 0 Hz und 512 kHz.

C: 0 Hz und 1024 kHz.

D: -10 MHz und +10 MHz.

Latenz

Verzögerungen in der Signalübertragung

  • Bei der Signalübertragung und -verarbeitung entstehen Verzögerungen
  • Lichtgeschwindigkeit: Zeit, die elektromagnetische Wellen vom Sender zum Empfänger benötigen
  • Weitere Verzögerungen durch Zwischenspeicherung (Buffer) und Filter

Latenz in der Signalverarbeitung

  • Laufzeit zwischen Sender und Empfänger oder zwischen Verarbeitungsstufen
  • Latenz wird in Sekunden gemessen
  • Typische Werte: wenige Millisekunden bis einige Sekunden
  • Analoge Verfahren haben oft geringere Latenzen als digitale, da weniger Zwischenspeicherung erfolgt
AF637: Was wird in der digitalen Signalverarbeitung unter Latenz verstanden und in welcher Einheit kann sie angegeben werden?

A: Geschwindigkeit eines Signals in Metern pro Sekunde

B: Schwankung der Amplitude eines Signals in Volt pro Sekunde

C: Schwankung der Frequenz eines Signals in Hertz pro Sekunde

D: Laufzeit bzw. Verzögerung eines Signals in Sekunden

Fragen?

Links zu diesem Foliensatz