Empfänger
Navigationshilfe
Diese Navigationshilfe zeigt die ersten Schritte zur Verwendung der Präsentation. Sie kann mit ⟶ (Pfeiltaste rechts) übersprungen werden.
Navigation
Zwischen den Folien und Abschnitten kann man mittels der Pfeiltasten hin- und herspringen, dazu kann man auch die Pfeiltasten am Computer nutzen.

- Pfeil runter und hoch: Nächste / Vorherige Folie
- Pfeil rechts und links: Nächster / Vorheriger Abschnitt
- Leertaste oder „n“: Der Reihe nach alle Elemente in Folien aufdecken oder zur nächsten Folie blättern
- Shift-Leertaste oder „p“: Der Reihe nach Elemente rückwärts zudecken oder zur vorherigen Folie blättern
Weitere Funktionen
Mit ein paar Tastenkürzeln können weitere Funktionen aufgerufen werden. Die wichtigsten sind:
- F1
- Help / Hilfe
- o
- Overview / Übersicht aller Folien
- s
- Speaker View / Referentenansicht
- f
- Full Screen / Vollbildmodus
- b
- Break, Black, Pause / Ausblenden der Präsentation
- Alt-Click
- In die Folie hin- oder herauszoomen
Übersicht
Die Präsentation ist zweidimensional aufgebaut. Dadurch sind in Spalten die einzelnen Abschnitte eines Kapitels und in den Reihen die Folien zu den Abschnitten.
Tippt man ein „o“ ein, bekommt man eine Übersicht über alle Folien des jeweiligen Kapitels. Das hilft sich zunächst einen Überblick zu verschaffen oder sich zu orientieren, wenn man das Gefühlt hat sich „verlaufen“ zu haben. Die Navigation erfolgt über die Pfeiltasten.

Durch Anklicken einer Folie wird diese präsentiert.
Referentenansicht
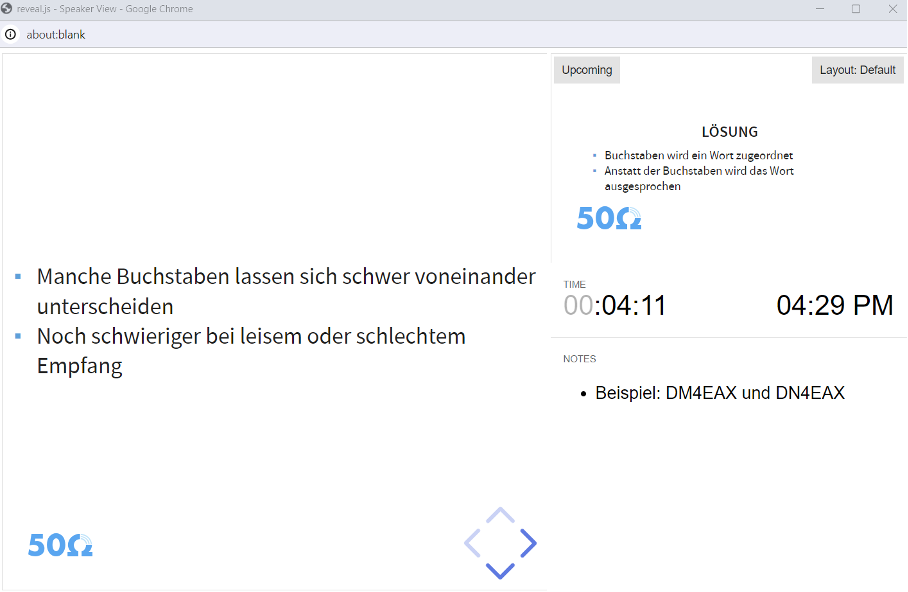
Tippt man ein „s“ ein, bekommt man ein neues Fenster, die Referentenansicht.
Indem man „Layout“ auswählt, kann man zwischen verschieden Anordnungen der Elemente auswählen.
Die Referentenansicht bietet folgende Elemente:
- Links sieht man die aktuelle Folie
- Rechts oben sieht man die nächste Folie
- Rechts in der Mitte Hilfsmittel zur Zeiteinteilung
- Rechts unten, die „Notizen für den Vortragenden“
- Unten die Pfeile zur Navigation
Praxistipps zur Referentenansicht
- Wenn man mit einem Projektor arbeitet, stellt man im Betriebssystem die Nutzung von 2 Monitoren ein: Die Referentenansicht wird dann zum Beispiel auf dem Laptop angezeigt, während die Teilnehmer die Präsentation angezeigt bekommen.
- Bei einer Online-Präsentation, wie beispielsweise auf TREFF.darc.de präsentiert man den Browser-Tab und navigiert im „Speaker View“ Fenster.
- Die Referentenansicht bezieht sich immer auf ein Kapitel. Am Ende des Kapitels muss sie geschlossen werden, um im neuen Kapitel eine neue Referentenansicht zu öffnen.
- Um mit dem Mauszeiger etwas zu markieren oder den Zoom zu verwenden, muss mit der Maus auf den Bildschirm mit der Präsentation gewechselt werden.
Vollbild
Tippt man ein „f“ ein, wird die aktuelle Folie im Vollbild angezeigt. Mit „Esc“ kann man diesen wieder verlassen.
Das ist insbesondere für den Bildschirm mit der Präsentation für das Publikum praktisch.
Ausblenden
Tippt man ein „b“ ein, wird die Präsentation ausgeblendet.
Sie kann wie folgt wieder eingeblendet werden:
- Durch klicken in das Fenster.
- Durch nochmaliges Drücken von „b“.
- Durch klicken der Schaltfläche „Resume presentation:

Zoom
Bei gedrückter Alt-Taste und einem Mausklick in der Präsentation wird in diesen Teil hineingezoomt. Das ist praktisch, um Details von Schaltungen hervorzuheben. Durch einen nochmaligen Mausklick zusammen mit Alt wird wieder herausgezoomt.
Das Zoomen funktioniert nur im ausgewählten Fenster. Die Referentenansicht ist hier nicht mit dem Präsenationsansicht gesynct.
Überlagerungsempfänger (Einfachsuper) II
Nahselektion oder Trennschärfe
- Fähigkeit des Empfängers, das gewünschte Empfangssignal möglichst gut von benachbarten Signalen trennen zu können
- Wird maßgeblich durch die ZF-Filter bestimmt
- Legt die Qualität des gesamten Empfangszweiges fest
A: Durch die ZF-Filter
B: Durch den Bandpass auf der Empfangsfrequenz
C: Durch die ZF-Verstärkung
D: Durch den Empfangsvorverstärker
Mischer II
Steuerkennlinien
Steuerkennlinien können linear oder nicht-linear sein
- Im linearen Bereich finden keine Verzerrungen statt
- Mathematisches Verhalten wie bei Addition
- Im nichtlinearen Bereich bewirkt die Steuerkennlinie die Verzerrung von einem Eingangssignal zu unterschiedlichen Änderungen am Ausgangssignal
- Mathematischen Verhalten wie bei einer Multiplikation
- Deshalb findet im nichtlinearen Bereich immer ein Mischprozess statt
- Mischprodukte erzeugen immer zusätzliche Frequenzen im Ausgangssignal
A: Sie arbeitet im kapazitiven Bereich.
B: Sie arbeitet im induktiven Bereich.
C: Sie arbeitet im nichtlinearen Bereich.
D: Sie arbeitet im linearen Bereich.
Ringmischer
- Am Ausgang eines Mischers soll nur das Mischprodukt erscheinen
- Unerwünschte Mischprodukte und die Eingangssignale sollen maximal unterdrückt werden
- 4 Dioden in Ringschaltung
- Oszillator an U2 schaltet immer zwei Dioden aktiv
- In dieser Zeit kann eine gleichförmige Welle von U1 zum Ausgang gelangen
A: Dualtransistormischer
B: Balancemischer
C: additiver Diodenmischer
D: Doppeldiodenmischer
A: Ein additiver Diodenmischer
B: Ein balancierter Ringmischer
C: Ein unbalancierter Produktdetektor
D: Ein Eintakt-Transistormischer
Spiegelfrequenzen
$f_{ZF} = \left|f_e \pm f_o\right|$
Im Mischprozess zur $f_{ZF}$ werden prinzipbedingt immer zwei Empfangsfrequenzen ausgewählt
- Gewünschte Empfangsfrequenz $f_{e1}$ → Spiegelfrequenz $f_{e2}$
- Abstand zwischen gewünschter Empfangsfrequenz und Spiegelfrequenz → ${2 \cdot f_{ZF}}$
Oszillator schwingt oberhalb der Empfangsfrequenz
↓
Spiegelfrequenz bei ${2 \cdot f_{ZF}}$ oberhalb der Empfangsfrequenz
Oszillator schwingt unterhalb der Empfangsfrequenz
↓
Spiegelfrequenz bei ${2 \cdot f_{ZF}}$ unterhalb der Empfangsfrequenz
$$f_S = 2 \cdot f_{OSZ}\,-\,f_E =\\ \begin{cases}f_{OSZ}\,+\,f_{ZF} = f_E\,+\,2 \cdot f_{ZF} &\text{wenn } f_E \lt f_{OSZ} \\ f_{OSZ}\,-\,f_{ZF} = f_E\,-\,2 \cdot f_{ZF} &\text{wenn } f_E \gt f_{OSZ} \end{cases}$$
Spiegelfrequenzunterdrückung
- Ohne Unterdrückung kann die Spiegelfrequenz zu Empfangsstörungen führen
- Vermeidung: Gewünschte Frequenz wird durch einen Bandpassfilter selektiert
- Spiegelfrequenz wird möglichst maximal unterdrückt
Maßnahme für eine möglichst hohe Unterdrückung:
- Abstand zwischen gewünschter Empfangsfrequenz und Spiegelfrequenz durch eine hohe ZF möglichst groß wählen
- Bei einem großen Abstand kann ein hochwertiges Bandpassfilter leichter realisiert werden
A: Die HF-Nutzfrequenz plus der ZF
B: Das Dreifache der ZF
C: Das Doppelte der HF-Nutzfrequenz
D: Das Doppelte der ZF
A:
B:
C:
D:
Lösungsweg
- gegeben: $f_{OSZ} = 134,9MHz$
- gegeben: $f_E = 145,6MHz$
- gesucht: $f_S$
$\begin{aligned}f_S &= 2 \cdot f_{OSZ} – f_E\\ &= 2 \cdot 134,9MHz – 145,6MHz\\ &= 124,2MHz\end{aligned}$
A:
B:
C:
D:
Lösungsweg
- gegeben: $f_{OSZ} = 39MHz$
- gegeben: $f_E = 28,3MHz$
- gesucht: $f_S$
$\begin{aligned}f_S &= 2 \cdot f_{OSZ} – f_E\\ &= 2 \cdot 39MHz – 28,3MHz\\ &= 49,7MHz\end{aligned}$
A: Durch die Demodulatorkennlinie
B: Durch die Selektion im ZF-Bereich
C: Durch den Tiefpass im Audioverstärker
D: Durch die Vorselektion
A: Die doppelte ZF
B: Die doppelte Empfangsfrequenz
C: Die ZF
D: Die Frequenz des lokalen Oszillators
A:
B:
C:
D:
Lösungsweg
- gegeben: $f_{OSZ} = 24,94MHz$
- gegeben: $f_E = 14,24MHz$
- gesucht: $f_S$
$\begin{aligned}f_S &= 2 \cdot f_{OSZ} – f_E\\ &= 2 \cdot 24,94MHz – 14,24MHz\\ &= 35,64MHz\end{aligned}$
A:
B:
C:
D:
Lösungsweg
- gegeben: $f_{ZF} = 10,7MHz$
- gegeben: $f_E = 28,5MHz$
- gesucht: $f_S$
Bei $f_E < f_{OSZ}$:
$\begin{aligned}f_S &= f_E + 2 \cdot f_{ZF}\\ &= 28,5MHz + 2 \cdot 10,7MHz\\ &= 49,9MHz\end{aligned}$
A: Ein solcher Empfänger hat eine höhere Großsignalfestigkeit.
B: Man erhält einen Empfänger für Kurzwelle und gleichzeitig für Ultrakurzwelle.
C: Die Spiegelfrequenz liegt sehr weit außerhalb des Empfangsbereichs.
D: Filter für
A: Durch die NF-Bandbreite
B: Durch die Bandbreite der ZF-Filter
C: Durch die Verstärkung der ZF
D: Durch die Höhe der ZF
A: Sie ermöglicht eine hohe Spiegelfrequenzunterdrückung.
B: Sie vermeidet eine hohe Spiegelfrequenzunterdrückung.
C: Sie ermöglicht eine gute Nahselektion.
D: Sie reduziert Beeinflussungen des lokalen Oszillators durch Empfangssignale.
Doppelüberlagerungsempfänger (Doppelsuper)
- HF-Teil mit Vorselektion
- 1. Mischer mit VFO
- 1. ZF-Verstärker mit Roofing-Filter
- 2. Mischer mit CO
- 2. ZF-Verstärker mit Filter
- 3. Mischer als Produktdetektor oder Demodulator ggf. mit BFO
- NF-Verstärker
- Verwendung von zwei Zwischenfrequenzen
- Hohe 1. ZF → gute Spiegelfrequenzunterdrückung
- Niedrige 2. ZF → hohe Trennschärfe
- Nach 1. ZF ist ein Eingangsfilter vor 2. Mischer
- Spiegelfrequenz lässt sich durch großen Abstand gut unterdrücken
- Nach 2. ZF Filter mit hoher Güte
- Lässt sich für niedrige Frequenzen gut realisieren
- ZF und gewünschte Empfangsfrequenz weit entfernt legen → Vermeidung des Direktempfangs der ZF
- 1. ZF das Doppelte der maximalen Empfangsfrequenz
A: Mit einer niedrigen ersten ZF erreicht man leicht eine gute Spiegelfrequenzunterdrückung.
B: Das von der Antenne aufgenommene Signal bleibt bis zum Demodulator in seiner Frequenz erhalten.
C: Mit einer niedrigen zweiten ZF erreicht man leicht eine gute Spiegelfrequenzunterdrückung.
D: Mit einer hohen ersten ZF erreicht man leicht eine gute Spiegelfrequenzunterdrückung.
A: Durch eine hohe erste ZF erreicht man leicht eine hohe Empfindlichkeit.
B: Mit einer niedrigen ersten ZF erreicht man leicht gute Werte bei der Kreuzmodulation.
C: Durch eine niedrige zweite ZF erreicht man leicht eine gute Spiegelselektion.
D: Mit einer niedrigen zweiten ZF erreicht man leicht eine gute Trennschärfe.
A: Die 1. ZF liegt höher als das Doppelte der maximalen Empfangsfrequenz. Nach der Filterung im Roofing-Filter (1. ZF) wird auf eine niedrigere 2. ZF heruntergemischt.
B: Die 1. ZF liegt unter der niedrigsten Empfangsfrequenz. Die 2. ZF liegt über der höchsten Empfangsfrequenz.
C: Die 1. ZF darf maximal die Hälfte der höchsten Empfangsfrequenz betragen. Die 2. ZF liegt höher als das Doppelte der niedrigsten Empfangsfrequenz.
D: Die 1. ZF liegt niedriger als die maximale Empfangsfrequenz. Nach der Filterung im Roofing-Filter (1. ZF) wird auf eine höhere 2. ZF heraufgemischt.
Roofing Filter
- Nach 1. Mischer schmales Filter (Roofing Filter)
- Auf 1. ZF abgestimmt
- Bandbreite mindestens so groß wie größte benötigte Empfangsbandbreite
A: Mindestens so groß wie die größte benötigte Bandbreite der vorgesehenen Betriebsarten.
B: Mindestens so groß wie das breiteste zu empfangende Amateurband.
C: Sie muss den vollen Abstimmbereich des Empfängers umfassen.
D: Mindestens so groß wie die doppelte Bandbreite der jeweiligen Betriebsart.
A: X und Y sind Mischer, Z ist ein Produktdetektor.
B: X ist ein Mischer, Y ist ein Produktdetektor, Z ist ein Mischer.
C: X und Y sind Produktdetektoren, Z ist ein HF-Mischer.
D: X und Y sind Balancemischer, Z ist ein ZF-Verstärker.
A: X ist ein VFO, Y ist ein BFO und Z ein CO.
B: X ist ein BFO, Y ist ein VFO und Z ein CO.
C: X ist ein VFO, Y ist ein CO und Z ein BFO.
D: X ist ein BFO, Y ist ein CO und Z ein VFO.
Oszillator-Frequenzen
- Oszillatorfrequenzen sind jeweils ober- oder unterhalb der gewünschten Eingangsfrequenz
- Es existieren für jeden Mischer zwei Lösungsmöglichkeiten
- $f_{OSZ} = f_{ZF}\,+\,f_{E}$
- $f_{OSZ} = f_{ZF}\,-\,f_{E}$
A: 20 bis
B: 20 bis
C: 23 bis
D: 23 bis
Lösungsweg
- gegeben: $f_E = 3\dots30MHz$
- gegeben: $f_{ZF1} = 50MHz$
- gesucht: $f_{OSZ}$
$f_{ZF} = |f_E − f_{OSZ}| \Rightarrow f_{OSZ} = f_{ZF} \pm f_{E}$
- Lösung: $\begin{aligned}f_{OSZ} &= f_{ZF}\,+\,f_{E}\\ &= 50MHz\,+\,3\dots30MHz\\ &= 53\dots80MHz\end{aligned}$
- Lösung: $\begin{aligned}f_{OSZ} &= f_{ZF}\,-\,f_{E}\\ &= 50MHz\,-\,3\dots30MHz\\ &= 47\dots20MHz\end{aligned}$
A: VFO:
B: VFO:
C: VFO:
D: VFO:
Lösungsweg
- gegeben: $f_{E} = 3,65MHz$
- gegeben: $f_{ZF1} = 50MHz$
- gegeben: $f_{ZF2} = 9MHz$
- gegeben: $f_{NF} = 455kHz$
- gesucht: $f_{OSZ}$ für $f_{VFO}, f_{CO1}, f_{CO2}$
$f_{ZF1} = \begin{cases}f_E\,+\,f_{OSZ}\\ f_{OSZ}\,-\,f_E\\ f_E\,-\,f_{OSZ}\end{cases} \Rightarrow f_{OSZ} = \begin{cases}f_{ZF}\,-\,f_E\\ f_E\,+\,f_{ZF}\\ f_E\,-\,f_{ZF}\end{cases}$
$f_{VFO} = \begin{cases}f_{ZF1}\,-\,f_E = 50MHz\,-\,3,65MHz = 46,35MHz\\ f_E\,+\,f_{ZF1} = 3,65MHz\,+\,50MHz = 53,64MHz\\ f_E\,-\,f_{ZF1} = 3,65MHz\,-\,50MHz = \cancel{-46,35MHz}\end{cases}$
$f_{CO1} = \begin{cases}f_{ZF2}\,-\,f_{ZF1} = 9MHz\,-\,50MHz = \cancel{-41MHz}\\ f_{ZF1}\,+\,f_{ZF2} = 50MHz\,+\,9MHz = 59MHz\\ f_{ZF1}\,-\,f_{ZF2} = 50MHz\,-\,9MHz = 41MHz\end{cases}$
$f_{CO2} = \begin{cases}f_{NF}\,-\,f_{ZF2} = 455kHz\,-\,9MHz = \cancel{-8,545MHz}\\ f_{ZF2}\,+\,f_{NF} = 9MHz\,+\,455kHz = 9,455MHz\\ f_{ZF2}\,-\,f_{NF} = 9MHz\,-\,455kHz = 8,545MHz\end{cases}$
VFO: $\bold{46,35MHz} \And 53,65MHz$, CO1: $\bold{41MHz} \And 59MHz$, CO2: $8,545MHz \And \bold{9,455MHz}$
A: Der VFO muss bei
B: Der VFO muss bei
C: Der VFO muss bei
D: Der VFO muss bei
Lösungsweg
- gegeben: $f_{E} = 21,1MHz$
- gegeben: $f_{ZF1} = 9MHz$
- gegeben: $f_{ZF2} = 460kHz$
- gesucht: $f_{VFO} \gt f_E, f_{CO} \lt f_{ZF1}$
$f_{ZF} = \begin{cases}f_{OSZ}\,-\,f_E\\ f_E\,-\,f_{OSZ}\end{cases} \Rightarrow f_{OSZ} = \begin{cases}f_E\,+\,f_{ZF}\\ f_E\,-\,f_{ZF}\end{cases}$
$f_{VFO} = f_E\,+\,f_{ZF1} = 21,1MHz\,+\,9MHz = 30,1MHz$
$f_{CO} = f_{ZF1}\,-\,f_{ZF2} = 9MHz\,-\,460kHz = 8,54MHz$
A: Der VFO muss bei
B: Der VFO muss bei
C: Der VFO muss bei
D: Der VFO muss bei
Lösungsweg
- gegeben: $f_{E} = 28MHz$
- gegeben: $f_{ZF1} = 10,7MHz$
- gegeben: $f_{ZF2} = 460kHz$
- gesucht: $f_{VFO} \gt f_E, f_{CO} \gt f_{ZF1}$
$f_{ZF} = \begin{cases}f_{OSZ}\,-\,f_E\\ f_E\,-\,f_{OSZ}\end{cases} \Rightarrow f_{OSZ} = \begin{cases}f_E\,+\,f_{ZF}\\ f_E\,-\,f_{ZF}\end{cases}$
$f_{VFO} = f_E\,+\,f_{ZF1} = 28MHz\,+\,10,7MHz = 38,70MHz$
$f_{CO} = f_{ZF1}\,+\,f_{ZF2} = 10,7MHz\,+\,460kHz = 11,16MHz$
Trennschärfe II
- Trennschärfe eines Empfängers wird durch die Bandbreite der Filter im ZF-Bereich bestimmt
- Bandbreite ist nach Modulationsart unterschiedlich
- SSB →
2,7 kHz - CW und RTTY →
500 Hz zur Trennung von nebenliegenden Signalen - FM →
12 kHz
- Bandbreiten und Flankensteilheit durch technisch unterschiedliche Konzepte
- Quarzfilter → stark steilflankig und sehr schmalbandig
- Keramikfilter → steilflankig und schmalbandig
- LC-Filter → nicht so steilflankig und größere Bandbreite
- RC-Filter werden üblicherweise in HF nicht eingsetzt
A: LC-Filter
B: RC-Filter
C: Quarzfilter
D: Keramikfilter
A: SSB:
B: SSB:
C: SSB:
D: SSB:
A: Das Oberwellenfilter im ZF-Verstärker
B: Der Oszillatorschwingkreis in der Mischstufe
C: Die PLL-Frequenzaufbereitung
D: Die Filter im ZF-Verstärker
A: AM-Signale
B: FM-Signale
C: SSB-Signale
D: OFDM-Signale
BFO II
BFO für SSB
- Beat-Frequency-Oszillator (BFO) schwingt genau auf der Frequenz des unterdrückten Trägers
- Mischt den Träger wieder rein
- Möglichst hohe Frequenzstabilität → Quarzgesteuerter Oszillator
BFO für CW
- BFO muss Abstand zum CW-Signal haben
- So viel, wie das hörbare CW-Signal sein soll
- Angenehmer Ton bei 600 bis
900 Hz - Meistens bei
800 Hz
A: die halbe Zwischenfrequenz
B:
C:
D: die doppelte Zwischenfrequenz
A: quarzgesteuerter Oszillator
B: LC-Oszillator mit Reihenschwingkreis
C: RC-Oszillator
D: LC-Oszillator mit Parallelschwingkreis
Inter- und Kreuzmodulation
- Zwei starke HF-Signale am Eingang eines Empfängers → Störungen durch Inter- oder Kreuzmodulation
- Bei Intermodulation zeigt die Empfängerstufe nichtlineares Verhalten → unerwünschte Frequenzen mit Überlagerungsstörungen
- Bei Kreuzmodulation wird gewünschtes Signal durch ein starkes, benachbartes AM-Signal beeinflusst → Modulation des benachbarten Senders ist hörbar
A: Frequenzmodulation
B: Intermodulation
C: erhöhter Signal-Rausch-Abstand
D: Dopplereffekt
A: Durch Reflexion der Oberwellen im Empfangsverstärker.
B: Durch die Übersteuerung eines Verstärkers.
C: Durch Übermodulation oder zu großen Hub.
D: Durch Vermischung eines starken unerwünschten Signals mit dem Nutzsignal.
A: Durch Batteriebetrieb des Empfängers
B: Durch starke HF-Signale auf einer sehr nahen Frequenz
C: Durch eine zu niedrige Rauschzahl des Empfängers
D: Durch Betrieb des Empfängers an einem linear geregelten Netzteil
A: Die HF-Stufe wird bei zunehmend großen Eingangssignalen zunehmend nichtlinear.
B: Der Empfänger ist nicht genau auf die Frequenz eingestellt.
C: Es wird ein zu schmalbandiger Preselektor verwendet.
D: Es wird ein zu schmalbandiges Quarzfilter verwendet.
Saugkreis
- Unterdrückung des Störsignals vor dem Empfänger
- Filter ist auf die Frequenz des Störsignals abgestimmt
- Störsignal wird unterdrückt
Großsignalfestigkeit IP3
- Interception Point IP3
- Maß für den Punkt, an dem unerwünschte Mischprodukte 3. Ordnung den Amplitudenwert des Eingangssignal erreichen
- Je höher der IP3 eines Empfängers, umso größere Signale können störungsfrei verarbeitet werden
A: Signal-Rausch-Verhältnis
B: Grenzempfindlichkeit
C: Trennschärfe
D: Großsignalfestigkeit
Attenuator
- Zuschaltbares Dämpfungsglied am Empfängereingang
- Intermodulationsprodukte und Kreuzmodulation werden verringert
- Nutzsignal wird um den Faktor des Dämpfungsglieds reduziert
- Störsignale auf den Faktor 1000 (3. Ordnung) abgeschwächt
- Beispiel: Attenuator 10dB → Nutzsignal 10dB → Mischprodukte 30dB
A: Einschalten der Rauschsperre
B: Einschalten eines Dämpfungsgliedes vor den Empfängereingang
C: Einschalten des Noise-Blankers
D: Einschalten des Vorverstärkers
Begrenzerverstärker
- Anwendung in der ZF bei FM
- Eingangssignal wird verstärkt
- Anschließend die Amplituden begrenzt
- Information ist in der Frequenzänderung weiterhin vorhanden
- Amplitudenschwankungen werden unterdrückt
A: Er bewirkt eine vollständige ZF-Trägerunterdrückung zur Vermeidung von AM-Störungen.
B: Er verringert das Vorstufenrauschen.
C: Er begrenzt das Ausgangssignal ab einem bestimmten Pegel des Eingangssignals zur Unterdrückung von AM-Störungen.
D: Er begrenzt den Hub für den FM-Demodulator.
Low Noise Block (LNB)
- Low Noise Block Converter (LNB) mischt hohe Frequenzen direkt hinter der Antenne herunter
- Häufig im Satellitenfunkverkehr
- Weniger Kabelverluste durch niedrige Frequenz
A: Der LNB demoduliert das Signal. Die entstehende NF ist unempfindlich gegen Kabeldämpfung.
B: Durch die Fernspeisespannung, die den LNB versorgt, sinkt die Kabeldämpfung.
C: Der LNB verstärkt das Empfangssignal und mischt dieses auf eine niedrigere Frequenz, auf der die Kabeldämpfung geringer ist.
D: Durch die Mischung des Empfangssignals mit der TCXO-Frequenz wird nur noch das Basisband übertragen.
- Benötigt Spannungsversorgung
- Einsatz von BIAS-T
- Unterschiedliche Spannungen für unterschiedliche Polarisation
- Üblicherweise
12 V und18 V
A: Der LNB schaltet die Polarisation um.
B: Der LNB wird durch Überspannung beschädigt.
C: Der LNB schaltet den Empfangsbereich um.
D: Der LNB schaltet auf einen anderen Satelliten um.
S-Meter
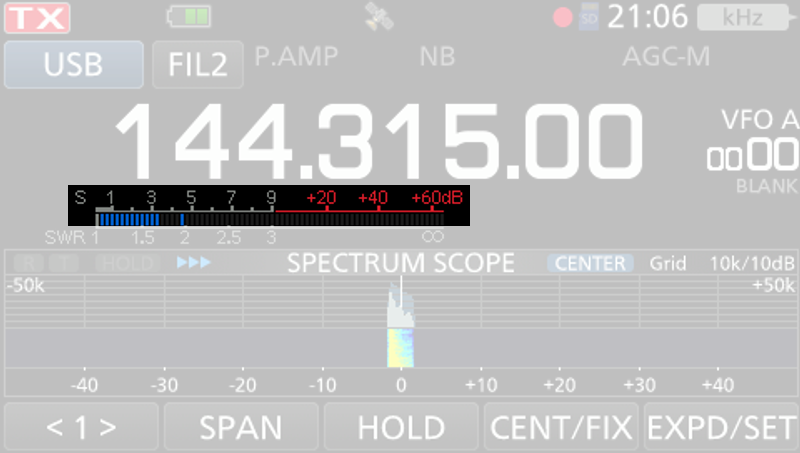
- Anzeige der Empfangsstärke des anliegenden HF-Signals
- 9 S-Stufen und nachfolgender Bereich mit +dB
- Bis S9: Eine S-Stufe entspricht 6dB
- 6dB: $2\cdot U$ oder $4\cdot P$
A:
B:
C:
D:
Lösungsweg
- von S3 bis S7 sind 3-Stufen
- $3\cdot 6dB = 18dB$
A: 100-fach
B: 10-fach
C: 120-fach
D: 20-fach
Lösungsweg
- von S7 auf S9+8dB sind 6dB+6dB+8dB = 20dB
- 20dB entsprechen der 100-fachen Leistung
A: Um acht S-Stufen
B: Um zwei S-Stufen
C: Um vier S-Stufen
D: Um eine S-Stufe
Lösungsweg
- von 25W auf 100W sind $\frac{100W}{25W} = 4$-fache Leistung
- 4-fache Leistung entsprich einer S-Stufe
A: Um vier S-Stufen
B: Um acht S-Stufen
C: Um eine S-Stufe
D: Um zwei S-Stufen
Lösungsweg
- von 100W auf 400W sind $\frac{400W}{100W} = 4$-fache Leistung
- 4-fache Leistung entspricht einer S-Stufe
A: S9
B: S9+
C: S9+
D: S9+
Lösungsweg
- von 10W auf 100W sind $\frac{100W}{10W} = 10$-fache Leistung
- 10-fache Leistung entspricht 10dB
- von S8 auf S9 sind 6dB
- die restlichen 4dB kommen als +4dB oben drauf
A:
B:
C:
D:
Lösungsweg
- von S9+20dB auf S8 sind 26dB
Spannung am Eingang
- Kurzwelle bis
30 MHz : S9 ⇒ 50 µV an 50 Ω - VHF bei
144 MHz : S9 ⇒ 5 µV an 50 Ω
A:
B:
C:
D:
Lösungsweg
- von S9 auf S8 sind 6dB
- Das ist die halbe Spannung
- $\frac{50µV}{2} = 25µV$
Dämpfungsglieder
- Schwächen Signalpegel definiert ab
- Vermeidung von Übersteuerung oder Beschädigung von Messgeräten
- Eingangspegel für Verstärker und Empfänger auf ein definiertes Maß reduzieren
- Dämpfung über Widerstände und Umwandlung in Wärme
- Bei symmetrischen Dämpfungsgliedern sind Ein- und Ausgangsimpedanzen gleich
- Üblicherweise 50 Ω
- Dämpfung wird in dB angegeben
- z.B 20dB = Faktor 100
100 W Eingangsleistung ⇒1 W Ausgangsleistung
A:
B:
C:
D:
Lösungsweg
- gegeben: $P_1 = 100W$
- gegeben: $a = 20dB$
- gesucht: $\Delta P = P_2 – P_1$
$$\begin{align}\nonumber a &= 10 \cdot \log_{10}{(\frac{P_1}{P_2})}dB\\ \nonumber \Rightarrow \frac{a}{10} &= \log_{10}{(\frac{P_1}{P_2})}dB\\ \nonumber \Rightarrow 10^{\frac{a}{10}} &= \frac{P_1}{P_2}\\ \nonumber \Rightarrow P_2 &= \frac{P_1}{10^{\frac{a}{10}}}\end{align}$$
$P_2 = \frac{P_1}{10^{\frac{a}{10}}} = \frac{100W}{10^{\frac{20}{10}}} = 1W$
$\Delta P = P_2 – P_1 = 100W – 1W = 99W$
A: 10
B: 20
C: 100
D: 50
Lösungweg
- 20dB entsprechen einer Leistungdämpfung mit dem Faktor 100
A: 4
B: 3
C: 6
D: 2
Lösungsweg
- 6dB entsprechen einer Leistungsdämpfung mit dem Faktor 4
A: $R_1$ + $R_2$ +
B:
C: $R_1$ +
D:
Lösungsweg
- Die Impedanz für die Gesamtschaltung ändert sich nicht – also 50Ω
A: Hochpass
B: Verstärker
C: Dämpfungsglied
D: Tiefpass
A: Dämpfungsglied
B: Hochpass
C: Verstärker
D: Tiefpass
Automatische Verstärkungsregelung (AGC) II
- Starke Signale werden reduziert
- Leise Signale werden erhöht
- Amplitude des demodulierten Signals wird konstant gehalten
- → NF-Signal hat konstant gleiche Lautstärke
Ohne AGC
- Starke Signale übersteuern die NF
- Schwache Signale sind sehr leise
- Lautstärke muss von Hand nachgeregelt werden
A: Sie reduziert die Verstärkung von Verstärkerstufen im Empfangsteil.
B: Sie reduziert die Amplitude des VFO.
C: Sie erhöht die Verstärkung von Verstärkerstufen im Empfangsteil.
D: Sie reduziert die Amplitude des BFO.
SNR und Rauschzahl
SNR (Signal-to-Noise Ratio)
- Verhältnis von Nutzsignal zu Rauschsignal (Noise)
- Je höher das SNR, desto mehr hebt sich das Signal vom Rauschen ab
A: Es ist der Abstand zwischen Empfangsfrequenz und Spiegelfrequenz.
B: Er gibt an, in welchem Verhältnis das Rauschsignal stärker ist als das Nutzsignal.
C: Es ist der Frequenzabstand zwischen Empfangssignal und Störsignal.
D: Er gibt an, in welchem Verhältnis das Nutzsignal stärker ist als das Rauschsignal.
Rauschzahl
- Wird häufig bei HF-Vorverstärkern angegeben
- Verschlechterung des SNR bei Durchgang des Signals durch den Verstärker
- Verhältnis von eingehendem SNR zu ausgehendem SNR
- Rauschmaß: Angabe der Rauschzahl in dB
- Rauschzahl 2 → Rauschmaß 3dB
A: Das Rauschen des Ausgangssignals ist um
B: Das Ausgangssignal des Vorverstärkers hat ein um
C: Das Ausgangssignal des Vorverstärkers hat ein um
D: Die Verstärkung des Nutzsignals beträgt
A: Das Ausgangssignal des Verstärkers hat ein um
B: Das Ausgangssignal des Verstärkers hat ein um
C: Das Ausgangssignal des Verstärkers hat ein um
D: Das Ausgangssignal des Verstärkers hat ein um
Rauschen
- Das hörbare Rauschen ist von der Bandbreite des Empfängers abhängig
- Rauschleistung ist über die Bandbreiten berechenbar
- Bspw. bei Verwendung verschiedener Filter
$\Delta P_R = 10 \cdot \log_{10}{(\frac{B_1}{B_2})}dB$
A: Sie ist proportional zur Bandbreite des Empfängers.
B: Sie ist umgekehrt proportional zum Eingangswiderstand des Empfängers.
C: Sie ist proportional zum Signal-Rausch-Abstand des Empfängers
D: Sie ist umgekehrt proportional zur Bandbreite des Empfängers.
A: verringert sich um etwa
B: erhöht sich um etwa
C: erhöht sich um etwa
D: verringert sich um etwa
Lösungsweg
- gegeben: $B_1 = 2,5kHz$
- gegeben: $B_2 = 0,5kHz$
- gesucht: $\Delta P_R$
$\Delta P_R = 10 \cdot \log_{10}{(\frac{B_1}{B_2})}dB = 10 \cdot \log_{10}{(\frac{2,5kHz}{0,5kHz})}dB \approx 7dB$
Squelch II
- Vergleicht das empfangene Signal mit einem eingestellten Schwellwert
- Eingangssignal für Squelch wird an der ZF oder NF abgegriffen
A: Es ist das Signal des BFO.
B: Es ist das Signal des VFO.
C: Es ist das HF-Signal der Eingangsstufe.
D: Es sind die ZF- oder NF-Signale.
Demodulator
Demodulation von Signalen
- Demodulation wandelt ein moduliertes HF-Signal in ein hörbares NF-Signal um
- Abhängig von der verwendeten Modulation wird ein passendes Demodulationsverfahren gewählt
- Ziel: Wiederherstellung der ursprünglichen NF
AM-Demodulation
- AM-Signale werden mit einem Hüllkurvendemodulator verarbeitet
- HF-Signal wird über einen Schwingkreis selektiert und gleichgerichtet
- Kondensator lädt auf → Widerstand entlädt mit definierter Zeitkonstante
A: Produktdetektor zur Demodulation von SSB Signalen.
B: FM-Demodulator.
C: Hüllkurvendemodulator zur Demodulation von AM-Signalen.
D: SSB-Modulator.
- Anschluss X: Anzeige der gleichgerichteten Spitzenspannung
- Leichter Abfall der Spannung durch parallele Entladung
- Hüllkurve entspricht der aufmodulierten NF, überlagert mit einem Sägezahnsignal
- Nachfilterung entfernt den Trägeranteil
FM-Demodulation
- FM-Demodulation mittels Flankendiskriminator
- Signal aus der Zwischenfrequenz läuft in einen Schwingkreis
- Schwingkreis: Resonanzfrequenz \(f_\text{res}\) leicht versetzt zu \(f_\text{ZF}\)
- Frequenzänderungen werden in Amplitudenänderungen umgewandelt
- Nachgeschalteter AM-Demodulator liefert die NF
A: Produktdetektor zur Demodulation von FM-Signalen.
B: Diodendetektor zur Demodulation von SSB-Signalen.
C: Flanken-Diskriminator zur Demodulation von FM-Signalen.
D: Produktdetektor zur Demodulation von SSB-Signalen.
FM-Demodulation mittels PLL
- PLL nutzt einen spannungsgesteuerten Oszillator (VCO), der dem Eingangssignal folgt
- Regelspannung entspricht der FM-Modulation (aufmodulierte NF)
- Signalabgriff zur weiteren NF-Verarbeitung
A: PLL-Abwärtsmischer.
B: AM-Modulator.
C: PLL-FM-Demodulator.
D: SSB-Demodulator mit PLL-gesteuertem BFO.
SSB-Demodulation
- SSB-Demodulation mittels Produktdetektor
- Ringmischer mischt die Zwischenfrequenz (ZF) mit einem Beat Frequency Oscillator (BFO)
- Entstehendes Mischprodukt ist das gewünschte SSB-NF-Signal
- BFO muss exakt auf den unterdrückten Träger abgestimmt sein
A: Hüllkurvendemodulator zur Demodulation von AM-Signalen.
B: Flankendemodulator zur Demodulation von FM-Signalen.
C: Diskriminator zur Demodulation von FM-Signalen.
D: Produktdetektor zu Demodulation von SSB-Signalen.
Frequenzmessung II
Frequenzmessung bei Empfängern
- Empfangsfrequenz lässt sich meist nicht direkt messen, da kein Messpunkt vorhanden ist
- Zum Überprüfen wird ein genauer Oszillator oder Frequenzgenerator an die Antennenbuchse angeschlossen
- Vergleich der Generatorfrequenz mit der Empfängeranzeige
- GPS-disziplinierte Oszillatoren/OCXOs bieten höhere Genauigkeit
A: Mit einem Quarzofen- oder GPS-synchronisierten Frequenzgenerator.
B: Mit den Oberschwingungen eines konstant belasteten Schaltnetzteils.
C: Mit einem LC-Oszillator hoher Schwingkreisgüte.
D: Mit einem temperaturstabiliserten RC-Oszillator.
A: die Messdauer möglichst kurz gehalten wird.
B: der Hauptoszillator temperaturstabilisiert wird.
C: das Eingangssignal gleichgerichtet wird.
D: ein Vorteiler mit höherem Teilverhältnis benutzt wird.
Frequenzmessung bei Sendern
- Frequenzmessung bei Sendern ist einfacher
- Frequenzzähler wird über ein Dämpfungsglied an die Antennenbuchse angeschlossen
- Messung sinnvoll nur bei unmoduliertem Träger
A: Die Ausdehnung des Seitenbandes eines SSB-Senders
B: Den Modulationsindex eines FM-Senders
C: Die Sendefrequenz eines CW-Senders
D: Den Frequenzhub eines FM-Senders
A: der Zähler mit der Netzfrequenz zu synchronisieren.
B: der Zähler mit der Sendefrequenz zu synchronisieren.
C: eine analoge Modulation des Trägers zu verwenden.
D: ein Träger ohne Modulation zu verwenden.
- Die Frequenzmessung mittels Oszilloskop ist nur ein Notbehelf, da diese Geräte selten eine so genaue Zeitbasis wie Frequenzzähler haben.
A: Absorptionsfrequenzmesser und modulierter Träger
B: Frequenzzähler und unmodulierter Träger
C: Oszilloskop und unmodulierter Träger
D: Frequenzzähler und modulierter Träger
- Einfache Frequenzzähler arbeiten fast immer mit einer sogenannten Torzeit
- Das Gerät schaltet den Eingang für eine bestimmte Zeit ein, zählt die Perioden und berechnet daraus die Frequenz
- Eine Torzeit von 1 Sekunde liefert direkt die Frequenz in Hertz
- Kurze Torzeit: schnelle Aktualisierung
- Lange Torzeit: höhere Messgenauigkeit
A: die Auflösung.
B: die Langzeitstabilität.
C: die Stabilität.
D: die Empfindlichkeit.
Frequenzgenauigkeit
Genauigkeit von Frequenzen und Messbereichen
- Genauigkeitsangaben erfolgen in % (z.B. ${1 \cdot 10^{-2}}$) oder in parts per million (ppm = ${1 \cdot 10^{-6}}$)
- Manchmal wird auch direkt in Exponentialschreibweise angegeben, z.B. ${1 \cdot 10^{-7}}$
- Die angegebene Genauigkeit wird mit der Frequenz multipliziert, um die mögliche Abweichung von Messwerten oder Anzeigen zu berechnen
A:
B:
C:
D:
Lösungsweg
- gegeben: $f = 435MHz$
- gesucht: $1ppm$ von $f$
$435MHz \cdot \frac{1}{10^6} = \frac{435\cdot \cancel{10^6}Hz}{\cancel{10^6}} = 435Hz$
A: Zwischen 14,199986 bis
B: Zwischen 14,199858 bis
C: Zwischen 14,198580 bis
D: Zwischen 14,199990 bis
Lösungsweg Teil 1
- gegeben: $f = 14,200.000MHz$
- gegeben: $\textrm{Abw.} = 10ppm$
- gesucht: $f_{min}, f_{max}$
$\begin{aligned}f_{min} &= f\,-\,f \cdot \frac{10}{10^6}\\ &= 14,2MHz\,-\,\frac{14,2\cdot \cancel{10^6}Hz\cdot 10}{\cancel{10^6}}\\ &= 14,2MHz\,-\,142Hz\\ &= 14,199858MHz\end{aligned}$
Lösungsweg Teil 2
- gegeben: $f = 14,200.000MHz$
- gegeben: $\textrm{Abw.} = 10ppm$
- gesucht: $f_{min}, f_{max}$
$\begin{aligned}f_{max} &= f\,+\,f \cdot \frac{10}{10^6}\\ &= 14,2MHz\,+\,\frac{14,2\cdot \cancel{10^6}Hz\cdot 10}{\cancel{10^6}}\\ &= 14,2MHz\,+\,142Hz\\ &= 14,200142MHz\end{aligned}$
A:
B:
C:
D:
Lösungsweg
- gegeben: $f = 29MHz$
- gegeben: $\textrm{Abw.} = 0,01\%$
- gesucht: $\Delta f$
$\begin{aligned}\Delta f &= 29MHz \cdot 0,01\%\\ &= 29\cdot \cancel{10^6}Hz \cdot 100\cdot \cancel{10^{-6}}\\ &= 2900Hz\end{aligned}$
A: $±$
B: $±$
C: $±$
D: $±$
Lösungsweg
- gegeben: $f = 14100kHz$
- gegeben: $\textrm{Abw.} = \pm0,00001\%$
- gesucht: $\Delta f$
$\begin{aligned}\Delta f &= 14100kHz \cdot 0,00001\%\\ &= 14,1\cdot \cancel{10^6}Hz \cdot 0,1\cdot \cancel{10^{-6}}\\ &= 1,41Hz\end{aligned}$
A: $±$
B: $±$
C: $±$
D: $±$
Lösungsweg
- gegeben: $f = 100MHz$
- gegeben: $\textrm{Abw.} = \pm1ppm$
- gesucht: $\Delta f$
$\begin{aligned}\Delta f &= 100MHz \cdot \frac{1}{10^6}\\ &= \frac{100\cdot \cancel{10^6}Hz}{\cancel{10^6}}\\ &= 100Hz\end{aligned}$
A:
B:
C:
D:
Lösungsweg
- gegeben: $f = 145MHz$
- gegeben: $\textrm{Abw.} = 10ppm$
- gesucht: $f_{min},f_{max}$
$\begin{aligned}\Delta f &= 145MHz \cdot \frac{10}{10^6}\\ &= \frac{145\cdot \cancel{10^6}Hz \cdot 10}{\cancel{10^6}}\\ &= 1450Hz\end{aligned}$
$\begin{aligned}f_{min} &= f\,-\,\Delta f\\ &= 145MHz\,-\,1450Hz\\ &= 144,99855MHz\end{aligned}$
$\begin{aligned}f_{max} &= f\,+\,\Delta f\\ &= 145MHz\,+\,1450Hz\\ &= 145,00145MHz\end{aligned}$
A:
B:
C:
D:
Lösungsweg
- gegeben: $f = 144,400MHz$
- gegeben: $\textrm{Abw.} = 1ppm$
- gegeben: $f_{B,max} = 2,7kHz$
- gesucht: $f_{B,max,Abw}$
$\begin{aligned}\Delta f &= 144,4MHz \cdot \frac{1}{10^6}\\ &= \frac{144,4\cdot \cancel{10^6}Hz}{\cancel{10^6}}\\ &= 144,4Hz\end{aligned}$
$\begin{aligned}f_{B,max,Abw} &= f_{B,max} + \Delta f\\ &= 2,7kHz + 144,4Hz\\ &= 2,8444kHz\end{aligned}$