Strom- und Spannungsversorgung
Navigationshilfe
Diese Navigationshilfe zeigt die ersten Schritte zur Verwendung der Präsentation. Sie kann mit ⟶ (Pfeiltaste rechts) übersprungen werden.
Navigation
Zwischen den Folien und Abschnitten kann man mittels der Pfeiltasten hin- und herspringen, dazu kann man auch die Pfeiltasten am Computer nutzen.

- Pfeil runter und hoch: Nächste / Vorherige Folie
- Pfeil rechts und links: Nächster / Vorheriger Abschnitt
- Leertaste oder „n“: Der Reihe nach alle Elemente in Folien aufdecken oder zur nächsten Folie blättern
- Shift-Leertaste oder „p“: Der Reihe nach Elemente rückwärts zudecken oder zur vorherigen Folie blättern
Weitere Funktionen
Mit ein paar Tastenkürzeln können weitere Funktionen aufgerufen werden. Die wichtigsten sind:
- F1
- Help / Hilfe
- o
- Overview / Übersicht aller Folien
- s
- Speaker View / Referentenansicht
- f
- Full Screen / Vollbildmodus
- b
- Break, Black, Pause / Ausblenden der Präsentation
- Alt-Click
- In die Folie hin- oder herauszoomen
Übersicht
Die Präsentation ist zweidimensional aufgebaut. Dadurch sind in Spalten die einzelnen Abschnitte eines Kapitels und in den Reihen die Folien zu den Abschnitten.
Tippt man ein „o“ ein, bekommt man eine Übersicht über alle Folien des jeweiligen Kapitels. Das hilft sich zunächst einen Überblick zu verschaffen oder sich zu orientieren, wenn man das Gefühlt hat sich „verlaufen“ zu haben. Die Navigation erfolgt über die Pfeiltasten.

Durch Anklicken einer Folie wird diese präsentiert.
Referentenansicht
Tippt man ein „s“ ein, bekommt man ein neues Fenster, die Referentenansicht.
Indem man „Layout“ auswählt, kann man zwischen verschieden Anordnungen der Elemente auswählen.
Die Referentenansicht bietet folgende Elemente:
- Links sieht man die aktuelle Folie
- Rechts oben sieht man die nächste Folie
- Rechts in der Mitte Hilfsmittel zur Zeiteinteilung
- Rechts unten, die „Notizen für den Vortragenden“
- Unten die Pfeile zur Navigation
Praxistipps zur Referentenansicht
- Wenn man mit einem Projektor arbeitet, stellt man im Betriebssystem die Nutzung von 2 Monitoren ein: Die Referentenansicht wird dann zum Beispiel auf dem Laptop angezeigt, während die Teilnehmer die Präsentation angezeigt bekommen.
- Bei einer Online-Präsentation, wie beispielsweise auf TREFF.darc.de präsentiert man den Browser-Tab und navigiert im „Speaker View“ Fenster.
- Die Referentenansicht bezieht sich immer auf ein Kapitel. Am Ende des Kapitels muss sie geschlossen werden, um im neuen Kapitel eine neue Referentenansicht zu öffnen.
- Um mit dem Mauszeiger etwas zu markieren oder den Zoom zu verwenden, muss mit der Maus auf den Bildschirm mit der Präsentation gewechselt werden.
Vollbild
Tippt man ein „f“ ein, wird die aktuelle Folie im Vollbild angezeigt. Mit „Esc“ kann man diesen wieder verlassen.
Das ist insbesondere für den Bildschirm mit der Präsentation für das Publikum praktisch.
Ausblenden
Tippt man ein „b“ ein, wird die Präsentation ausgeblendet.
Sie kann wie folgt wieder eingeblendet werden:
- Durch klicken in das Fenster.
- Durch nochmaliges Drücken von „b“.
- Durch klicken der Schaltfläche „Resume presentation:

Zoom
Bei gedrückter Alt-Taste und einem Mausklick in der Präsentation wird in diesen Teil hineingezoomt. Das ist praktisch, um Details von Schaltungen hervorzuheben. Durch einen nochmaligen Mausklick zusammen mit Alt wird wieder herausgezoomt.
Das Zoomen funktioniert nur im ausgewählten Fenster. Die Referentenansicht ist hier nicht mit dem Präsenationsansicht gesynct.
Stromquellen
- Liefert konstanten Strom
- Unabhängig von der angeschlossenen Last
- Theorie: Unendlich großer Innenwiderstand
- Praxis: Sehr hoher Innenwiderstand
Anwendung einer Stromquelle
- Labornetzgeräte
- Ladetechnik von Akkus
Innenwiderstand
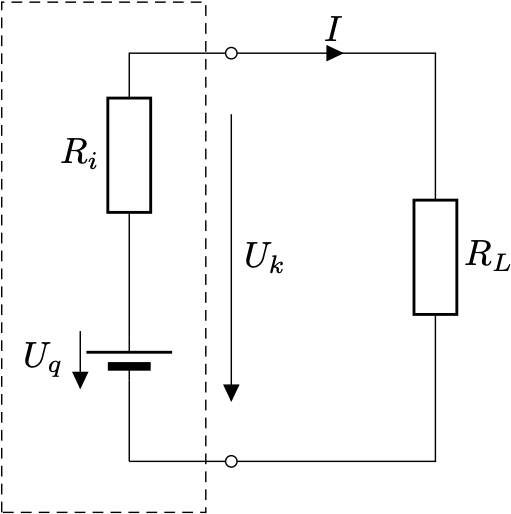
Spannungsquelle

- Reale Spannungsquelle wird mit $R_L$ belastet → Klemmenspannung $U_k$ sinkt
- Grund ist der Innenwiderstand
- Ohne Belastung / im Leerlauf: $U_q = U_L$
Innenwiderstand
- Nicht messbar mit einem Multimeter
- Rechnerisch ermitteln:
$R_i$ = $\frac{\Delta U}{\Delta I}$
- Leerlauf: $I = 0A$
- Belastung mit $R_L$:
$I_L = \frac{U_L}{R_L}$
Innenwiderstand Spannungsquelle
$(\Delta U = 0V)$; $R_i = \frac{\Delta U}{\Delta I} = \frac {0}{xxx} = 0\ \Omega$
Ideale Spannungsquellen sollen einen sehr niedrigen Innenwiderstand $R_i$$\ll$$R_L$ aufweisen, im Idealfall:
Strombegrenzung
- In Labornetzteilen eingebaut
- Laststrom übersteigt eine maximale Stromstärke
- → Klemmenspannung wird abgesenkt
- → Laststrom bleibt konstant
- Funktion der Konstantstromquelle
Innenwiderstand Stromquelle
$R_i = \frac{\Delta U}{\Delta I}$; $(\Delta I = „\textrm{Null}“ A)$; $R_i = \frac{\Delta U}{„\textrm{Null}“} = „\textrm{unendlich}“\ \Omega$
Ideale Stromquellen sollen einen sehr hohen Innenwiderstand $R_i$$\gg$$R_L$ aufweisen. Idealfall: „unendlich“ Ohm, dann bleibt der Laststrom bei Änderung des Lastwiderstandes konstant, deshalb spricht man auch von Stromanpassung.
A: Stromquellen sollten einen möglichst niedrigen Innenwiderstand und Spannungsquellen einen möglichst hohen Innenwiderstand haben.
B: Strom- und Spannungsquellen sollten einen möglichst hohen Innenwiderstand haben.
C: Stromquellen sollten einen möglichst hohen Innenwiderstand und Spannungsquellen einen möglichst niedrigen Innenwiderstand haben.
D: Strom- und Spannungsquellen sollten einen möglichst niedrigen Innenwiderstand haben.
Leistungsanpassung
- Optimale Leistungsabgabe von Sender zu Antenne
- $R_i = R_L$
| Zusammenfassung Innenwiderstand | Innenwiderstand |
|---|---|
| Spannungsanpassung bei einer Konstantspannungsquelle | $R_i$ = „sehr niederhohmig“ ; theoretisch $0\ \Omega$; $R_i$$\ll$$R_L$ identisch mit $R_L$$\gg$$R_i$ |
| Stromanpassung bei einer Konstantstromquelle | $R_i$ = „sehr hochohmig“ ; $R_i$$\gg$$R_L$ identisch mit $R_L$$\ll$$R_i$ |
| Leistungsanpassung bei Verstärkern | $R_L$ = $R_i$ |
A: 1/
B:
C:
D:
A: $R_\textrm{L} \ll R_\textrm{i}$
B: $R_\textrm{L} = \dfrac{1}{R_\textrm{i}}$
C: $R_\textrm{L} \gg R_\textrm{i}$
D: $R_\textrm{L} = R_\textrm{i}$
A: $R_{\textrm{L}} \gg R_{\textrm{i}}$
B: $R_{\textrm{L}} = \frac{1}{R_{\textrm{i}}}$
C: $R_{\textrm{L}} \ll R_{\textrm{i}}$
D: $R_{\textrm{L}} = R_{\textrm{i}}$
A: $R_{\textrm{L}} = \dfrac{1}{R_{\textrm{i}}}$
B: $R_{\textrm{L}} \gg R_{\textrm{i}}$
C: $R_{\textrm{L}} = R_{\textrm{i}}$
D: $R_{\textrm{L}} \ll R_{\textrm{i}}$
A:
B:
C:
D:
Lösungsweg
- gegeben: $U_0 = 13,5V$
- gegeben: $U_{Kl} = 13V$
- gegeben: $I = 2A$
- gesucht: $R_i$
$R_i = \frac{U_i}{I} = \frac{U_0-U_{Kl}}{I} = \frac{13,5V-13V}{2A} = 0,25Ω$
A:
B:
C:
D:
Lösungsweg
- gegeben: $U_0 = 13,8V$
- gegeben: $U_{Kl} = 13,6V$
- gegeben: $I = 20A$
- gesucht: $R_i$
$R_i = \frac{U_i}{I} = \frac{U_0-U_{Kl}}{I} = \frac{13,8V-13,6V}{20A} = 10mΩ$
A:
B:
C:
D:
Lösungsweg
- gegeben: $U_0 = 13,5V$
- gegeben: $U_{Kl} = 12,4V$
- gegeben: $I = 0,9A$
- gesucht: $R_i$
$R_i = \frac{U_i}{I} = \frac{U_0-U_{Kl}}{I} = \frac{13,5V-12,4V}{0,9A} = 1,22Ω$
A:
B:
C:
D:
Lösungsweg
- gegeben: $U_0 = 5,0V$
- gegeben: $U_{Kl} = 4,8V$
- gegeben: $R_L = 1,2Ω$
- gesucht: $R_i$
$I = \frac{U_{Kl}}{R_L} = \frac{4,8V}{1,2Ω} = 4A$
$R_i = \frac{U_i}{I} = \frac{U_0-U_{Kl}}{I} = \frac{5,0V-4,8V}{4A} = 0,05Ω$
Akkus
Akku-Typen
Die häufigsten Akku-Typen im Amateurfunk:
- Bleiakku (Pb)
- Nickel-Metallhydrid (NiMH)
- Lithium-Eisenphosphat (LiFePO4)

- Kapazität:
4200 mAh - Spannung: 4S1P /
13,2 V
- Entladung: 30C Constant / 40C Burst
- Balance-Stecker: JST-XH
Verschaltungen
Beispiele:
- 4S1P: 4 Zellen in Serie, 1 in Parallel
- 4S2P: 4 Zellen in Serie, 2 in Parallel
Pro Zelle ca. 3,2V bis 3,3V, also
$3,3V \cdot 4 = 13,2V$
Kapazität
Beispiel-Akku:
→ 1 Stunde mit
$t = \frac{Q}{I}$
$t = \frac{4,2Ah}{1A} = 1h$
Elektrische Energie
Gespeicherte elektrische Energie im Akku
$E = Q \cdot U$
Beispiel-Akku: $E = 4,2Ah \cdot 13,2V = 55,44Wh$
Entladestrom
Angabe auf dem Beispiel-Akku: 30C
Die Entladung kann mit 30 mal der Kapazität Q erfolgen
Entladestrom = $30\frac{1}{h} \cdot 4,2Ah = 126A$
Der Akku wäre in 128 Sekunden entladen.
Reihenschaltung von Akkus
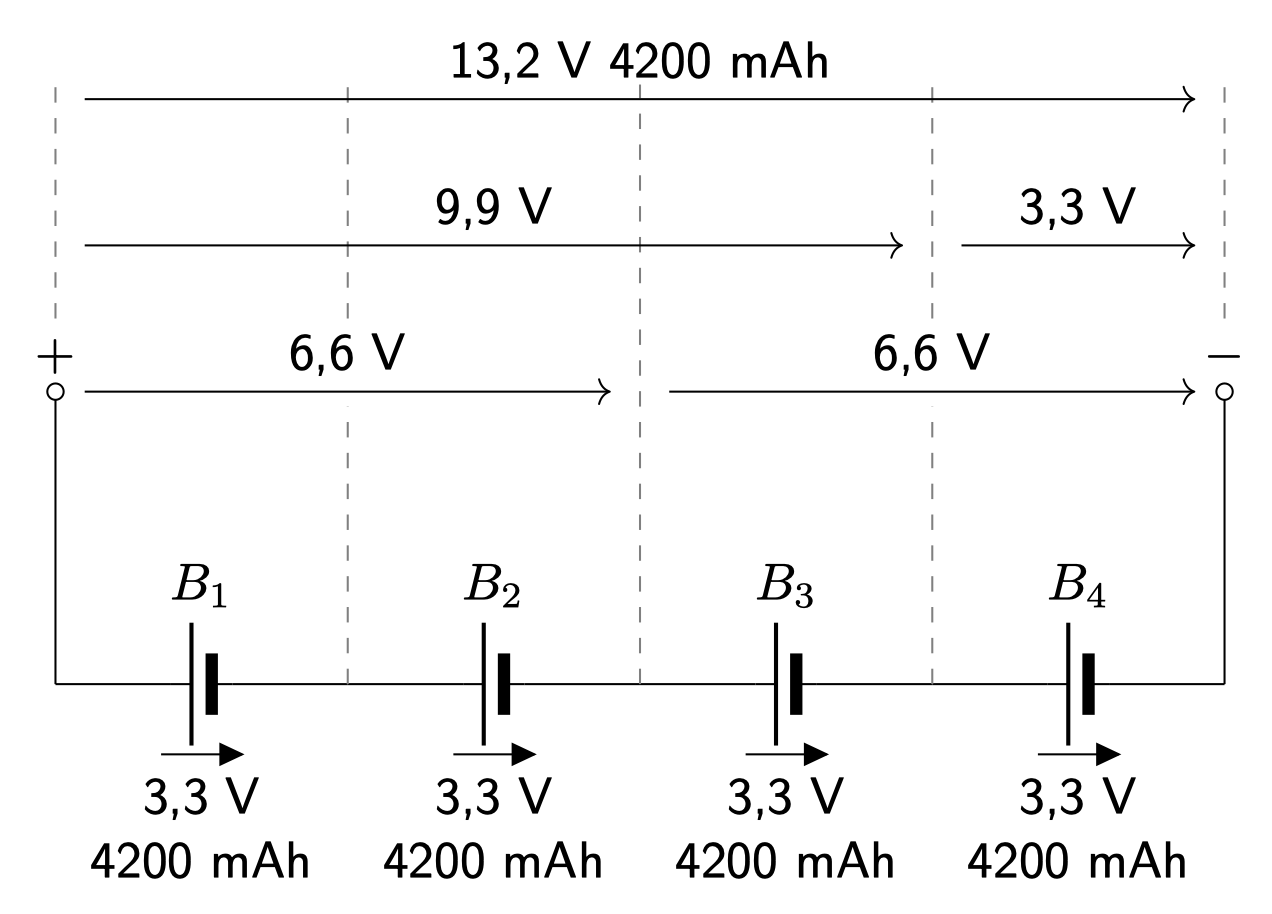
- Spannungen addieren sich
- Nur Zellen mit gleichen Daten zusammenschalten
Parallelschaltung von Akkus
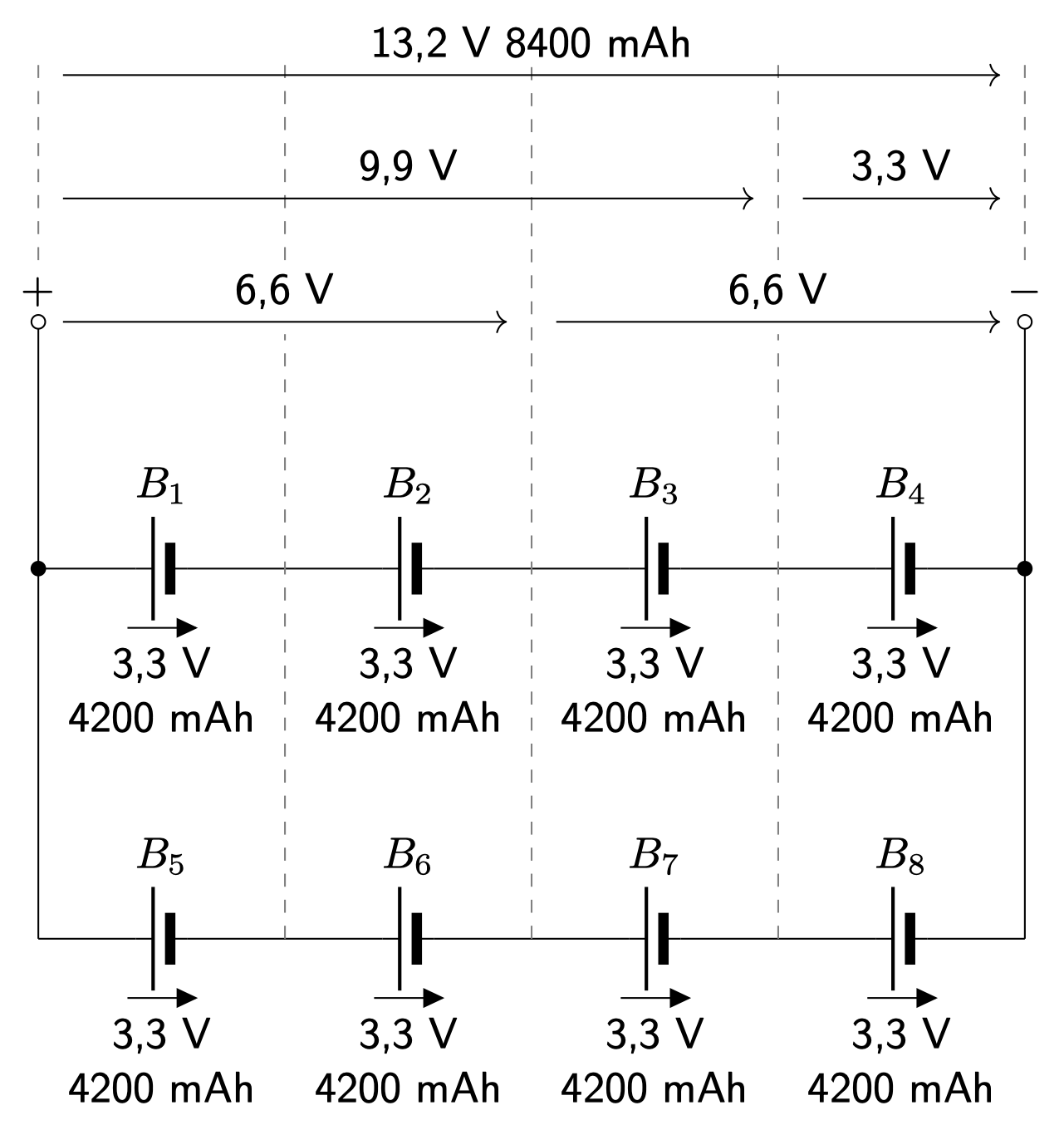
- Spannungen bleiben gleich
- Kapazitäten addieren sich
Balancer

- Balanceranschluss kann auf die Spannung jeder Zelle zugreifen
- Balancerschaltung zum Ausgleich der Spannungen
- Schutz der Zellen
- Batteriemonitor
A: Nennkapazität
B: maximaler Entladestrom pro Stunde
C: maximaler Ladestrom pro Stunde
D: Nennleistung
A:
B:
C:
D:
Lösungsweg
- gegeben: $U = 2V$
- gegeben: $Q = 10Ah$
- gegeben: $N = 6$
- gesucht: $U_{ges}, Q_{ges}$
$U_{ges} = N \cdot U = 6 \cdot 2V = 12V$
$Q_{ges} = Q \cdot 1 =10Ah$
A: 67 Stunden und 30 Minuten
B: 48 Stunden und 0 Minuten
C: 43 Stunden und 12 Minuten
D: 74 Stunden und 60 Minuten
Lösungsweg
- gegeben: $Q_{max} = 60Ah$
- gegeben: $Q_{10\%} = 0,1 \cdot Q_{max} = 6Ah$
- gegeben: $I = 0,8A$
- gesucht: $t$
$Q = I \cdot t \Rightarrow t = \frac{Q}{I} = \frac{Q_{max} – Q_{10\%}}{I} = \frac{54Ah}{0,8A} = 67,5h$
A:
B:
C:
D:
Lösungsweg
- gegeben: $U = 12V$
- gegeben: $Q = 5Ah$
- gesucht: $W$
$W = P \cdot t = U \cdot I \cdot t = U \cdot Q = 12V \cdot 5Ah = 60,0Wh$
Photovoltaik
- Solarzelle wandelt optische Strahlungsenergie in elektrische Energie um
- Grundsätzlicher Aufbau wie in einer Diode
- Durch die Strahlungsenergie werden Elektronen freigesetzt
- Bei Anschluss eines elektrischen Verbrauchers können diese fließen
A: Die Umwandlung von elektrischer Energie in Strahlungsenergie.
B: Die Umwandlung von thermischer Energie in Strahlungsenergie.
C: Die Umwandlung von Strahlungsenergie in elektrische Energie.
D: Die Umwandlung von Strahlungsenergie in thermische Energie.
Kenngrößen von Solarzellen
| Bezeichnung | Abkürzung | Erklärung |
|---|---|---|
| Leerlaufspannung | ${U}_{OC}$ | Ist die Spannung, die ohne Last bei voller Sonneneinstrahlung anliegt. |
| Kurzschlussstrom | ${I}_{SC}$ | Ist der Strom, welcher bei einem Kurzschluss am Ausgang, bei voller Sonneneinstrahlung, fließen wird. |
Zusammenschaltung von Solarzellen
Bei Reihen- und Parallelschaltung verändern sich Klemmenspannung und der maximale Laststrom
A: Leerlaufspannung:
B: Leerlaufspannung:
C: Leerlaufspannung:
D: Leerlaufspannung:
Lösungweg
- gegeben: $U_0 = 0,6V$
- gegeben: $I_k = 1A$
- gegeben: $N_R = 30, N_P = 4$
- gesucht: $U_{0,ges}, I_{k,ges}$
$U_{0,ges} = N_R \cdot U_0 = 30 \cdot 0,6V = 18V$
$I_{0,ges} = N_P \cdot I_k = 4 \cdot 1A = 4A$
Spannungswandler

- Wandelt Gleichspannungen um → DC/DC-Wandler
- z.B. von
13,8 V auf5 V → Step-DOWN (Tiefsetzsteller) - z.B. von
12 V auf19 V → Step-UP (Hochsetzsteller)
Wirkungsgrad
- Es entstehen Verluste durch die Bauteile in der Schaltung
- Wirkungsgrad $\eta$, meistens in $\%$ angegeben
$\eta = \frac{P_{\textrm{AB}}}{P_{\textrm{ZU}}}$
A: 62,5 %
B: 27,7 %
C: 41,7 %
D: 160 %
Lösungsweg
- gegeben: $U_{\textrm{ZU}} = 12V$
- gegeben: $U_{\textrm{AB}} = 5V$
- gegeben: $I_{\textrm{ZU}} = 2A$
- gegeben: $I_{\textrm{AB}} =3A$
- gesucht: $\eta$
$\eta = \frac{P_{\textrm{AB}}}{P_{\textrm{ZU}}} = \frac{U_{\textrm{AB}} \cdot I_{\textrm{AB}}}{U_{\textrm{ZU}} \cdot I_{\textrm{ZU}}} = \frac{5V \cdot 3A}{12V \cdot 2A} = \frac{15W}{24W} = 0,625 = 62,5\%$
A: 13,9 %
B: 125 %
C: 28,6 %
D: 80,0 %
- gegeben: $U_{\textrm{ZU}} = 5V$
- gegeben: $U_{\textrm{AB}} = 12V$
- gegeben: $I_{\textrm{ZU}} = 3A$
- gegeben: $I_{\textrm{AB}} =1A$
- gesucht: $\eta$
$\eta = \frac{P_{\textrm{AB}}}{P_{\textrm{ZU}}} = \frac{U_{\textrm{AB}} \cdot I_{\textrm{AB}}}{U_{\textrm{ZU}} \cdot I_{\textrm{ZU}}} = \frac{12V \cdot 1A}{5V \cdot 3A} = \frac{12W}{15W} = 0,8 = 80\%$
Gleichrichter II
- Bei positiver Halbwelle lässt Diode $D$ Strom fließen
- Lädt Kondensator $C_L$ auf Spitzenwert der Wechselspannung und versorgt Lastwiderstand $R_L$
- Bei negativer Halbwelle sperrt Diode $D$
- Kondensator $C_L$ entlädt sich über Lastwiderstand $R_L$
Am Lastwiderstand $R_L$ stellt sich eine pulsierende Gleichspannung $U_L$ ein
- Je größer die Kapazität, umso geglätteter die Gleichspannung
- Die Trafospannungen sind Effektivspannungen
- Für die Bemessung des Kondensators muss die Spitzenspannung bestimmt werden
- Für die Diode ist die Spitzen-Spitzen-Spannung relevant
A: Zirka
B: Zirka
C: Zirka
D: Zirka
Lösungsweg
- gegeben: $U_{eff} = 15V$
- gesucht: $\hat{U}$
$\hat{U} = U_{eff} \cdot \sqrt{2} = 15V \cdot 1,41 = 21,21V$
A:
B:
C:
D:
Lösungsweg
- gegeben: $U_P = 230V$
- gegeben: $\"{u} = 20:1$
- gesucht: $\hat{U} + 50\%$
$ü = \frac{U_P}{U_S} \Rightarrow U_S = \frac{U_P}{ü} = \frac{230V}{20} = 11,5V$
$\hat{U} = U_S \cdot \sqrt{2} = 11,5V \cdot 1,41 \approx 16,26V$
$\hat{U} + 50\% \approx 25V$
A:
B:
C:
D:
Lösungsweg
- gegeben: $U_P = 230V$
- gegeben: $\"{u} = 5:1$
- gesucht: $U_{SS} + 20\%$
$ü = \frac{U_P}{U_S} \Rightarrow U_S = \frac{U_P}{ü} = \frac{230V}{5} = 46V$
$\hat{U} = U_S \cdot \sqrt{2} = 46V \cdot 1,41 \approx 65,05V$
$U_{SS} + 20\% = 2 \cdot \hat{U} + 20\% \approx 156V$
Brückengleichrichter
- Erweiterte und häufige Gleichrichterschaltung
- Beide Halbwellen werden verwendet
- Pulsierende Gleichspannung am Ausgang mit doppelter Frequenz wie Eingangsspannung
Mit dem folgenden Applet kann man beide Halbperioden getrennt anschauen.
Siebung
- Mit Ladekondensator $C_L$ und LC-Siebglied mit $C_S$
- Kleinere Amplituden der pulsierenden Gleichspannung
- Kondensatoren laden sich auf die sekundäre Spitzenspannung auf
A: etwa
B: etwa
C: etwa
D: etwa
Lösungsweg
- gegeben: $U_P = 230V$
- gegeben: $\"{u} = 8:1$
- gegeben: $U_D = 0,6V$
- gesucht: $\hat{U}$
$ü = \frac{U_P}{U_S} \Rightarrow U_S = \frac{U_P}{ü} = \frac{230V}{8} = 28,75V$
Im Leerlauf kann die Diodenspannung vernachlässigt werden.
$\hat{U} = U_S \cdot \sqrt{2} = 28,75V \cdot 1,41 \approx 40V$
Vollweggleichrichter
Transformator mit Mittelanzapfung und zwei Dioden
- Positive Halbwelle an oberer Wicklung gegenüber Mittelanzapfung → $D_1$ leitet
- An $D_2$ liegt zu diesem Zeitpunkt eine negative Halbwelle an → sperrt
Mit dem folgenden Applet kann man beide Halbperioden getrennt anschauen.
Negative Ausgangsspannung
- Anoden sind an den Ausgang angeschlossen
- Gleichspannung wird gegenüber der Mittelanzapfung negativ
- Halbwellen befinden sich unterhalb der Nulllinie
Grundfrequenz
Nach der Gleichrichtung existiert eine pulsierende Gleichspannung mit doppelter Frequenz zur Eingangsspannung.
A:
B:
C:
D:
Restwelligkeit
- Keine Schaltung arbeitet ideal
- In einer Gleichrichterschaltung entsteht am Ausgang eine Gleichspannung mit einer überlagerten Wechselspannung → Restwelligkeit
- Kann mit einem Oszilloskop betrachtet werden
A:
B:
C:
D:
Schaltnetzteil II
- Elektronischer Schalter E regelt eine konstante Ausgangsspannung
- Schaltzeit wird variiert
- Schalter ist länger geschlossen → mehr Energie zur Lastseite → Ausgangsspannung steigt an
- Dieses ist der Impulsbreitenmodulator
A: Überspannungsableiter
B: Impulsbreitenmodulator
C: Gleichrichter
D: Puls-Gleichrichter
Galvanische Trennung
- Trennung der Eingangs- und Ausgangsseite
- Hält Störsignale der Schaltung von der Netzspannungseite fern
- Andernfalls wirkt das Stromnetz wie eine Antenne
A: Der Brückengleichrichter erzeugt eine Spannung mit Restwelligkeit.
B: Der elektronische Schalter in Block E erzeugt ein unerwünschtes Signalspektrum.
C: Die Diode am Ausgang muss hohe Frequenzen gleichrichten.
D: Der Transformator bewirkt hohe Verluste
A: unerwünschte Abstrahlungen eines linearen Netzteils.
B: einen schlecht entstörten Bürstenmotor.
C: unerwünschte Abstrahlungen eines Schaltnetzteils.
D: eine Amateurfunkstelle mit unzureichender Anpassung der Antenne.
Tiefpassfilter auf Eingangsseite

Spannungsstabilisierung
- Eingangsspannung kann variieren
- Beispielsweise bei durch Akku betriebenen Geräten
- Empfindliche Baugruppen (z.B. Oszillatoren) würden die Frequenz ändern
- Abhilfe: Spannungsstabilisierung
Stabilisierung mit Z-Diode
- Sehr einfache Schaltung
- Kann die Ausgangsspannung in Grenzen stabil halten
A: 0,34
B: 0,14
C: 0,17
D: 0,21
Lösungsweg
- gegeben: $R_L = 470Ω$
- gegeben: $I_L = 10mA$
- gegeben: $I_Z = 15mA$
- gegeben: $U_{IN} = 13,8V$
- gesucht: $\eta = \frac{P_L}{P_{IN}}$
$P_L = I_L^2 \cdot R_L = (10mA)^2 \cdot 470Ω = 47mW$
$P_{IN} = U_{IN} \cdot I_{IN} = U_{IN} \cdot (I_Z + I_L) = 13,8V \cdot (15mA + 10mA) = 345mW$
$\eta = \frac{P_L}{P_{IN}} = \frac{47mW}{345mW} \approx 0,14$
Linarer Spannungsregler
- Leistungstransistor wird als veränderlicher Widerstand betrieben
- Bildet zusammen mit dem Lastwiderstand einen Spannungsteiler
- Wirkungsgrad ist oft sehr niedrig
A:
B:
C:
D:
A:
B:
C:
D:
Lösungsweg
- gegeben: $U_{zu} = 13,8V$
- gegeben: $U_{ab} = 9V$
- gegeben: $I = 900mA$
- gesucht: $P_V$
$U_{IC1} = U_{zu} – U_{ab} = 13,8V – 9V = 4,8V$
$P_V = U_{IC1} \cdot I = 4,8V \cdot 900mA = 4,32W$
A: 0,99
B: 0,36
C: 0,56
D: 0,64
Lösungsweg
- gegeben: $U_{zu} = 13,8V$
- gegeben: $U_{ab} = 5V$
- gegeben: $I_{zu} = 455mA$
- gegeben: $I_{ab} = 450mA$
- gesucht: $\eta$
$\eta = \frac{P_{ab}}{P_{zu}} = \frac{U_{ab} \cdot I_{ab}}{U_{zu} \cdot I_{zu}} = \frac{5V \cdot 450mA}{13,8V \cdot 455mA} \approx 0,36$
Festspannungsregler
- Ausgelegt als IC
- Arbeiten wie linare Spannungsregler mit sehr genauer Spannungsreferenzquelle und optimaler elektronischer Regelung
- Auch bei starker Schwankung auf der Eingangsseite ist die Ausgangsseite sehr stabil
A: Die Spannungsschwankung beträgt ca.
B: Die Spannungsschwankung liegt zwischen
C: Die Spannungsschwankung beträgt nahezu null Volt.
D: Die Spannungsschwankung beträgt ca.
A: Die Eingangsspannung muss mindestens doppelt so groß wie die gewünschte Ausgangsspannung sein.
B: Die Eingangsspannung muss kleiner als die gewünschte Ausgangsspannung sein.
C: Die Eingangsspannung muss gleich der gewünschten Ausgangsspannung sein
D: Die Eingangsspannung muss größer als die gewünschte Ausgangsspannung sein.
A:
B:
C:
D:
Lösungsweg
- gegeben: $U_{zu} = 13,8V$
- gegeben: $U_{ab} = 5V$
- gegeben: $R_L = 10Ω$
- gesucht: $P_V$
$I = \frac{U_{zu}}{R_L} = \frac{5V}{10Ω} = 500mA$
$U_{IC1} = U_{zu} – U_{ab} = 13,8V – 5V = 8,8V$
$P_V = U_{IC1} \cdot I = 8,8V \cdot 500mA = 4,4W$
Fernspeiseweiche
- Englisch: BIAS-T
- Gleichspannungsübertragung auf einem Koaxialkabel gleichzeitig zum HF-Signal
- Spannungsversorgung von Baugruppen an der Antenne (z.B. LNA)
- Besteht aus nur drei Bauteilen
A: Zur Übertragung von zwei unterschiedlichen Gleichspannungen über eine gemeinsame Leitung.
B: Zur Verteilung eines HF-Signals auf zwei Ausgänge.
C: Zur Gleichspannungsversorgung und HF-Signalübertragung über eine gemeinsame Leitung.
D: Zur Verteilung der Gleichspannung auf zwei unterschiedliche Geräte.
A: Bias-T
B: PI-Filter
C: Netzfilter
D: Bandsperre
- $C_1$ hält das Gleichspannungssignal vom RX fern
- Fehlt $C_1$ wird die Gleichspannung gegen Masse kurzgeschlossen
- Gleichspannung wird über die Induktivität auf den Innenleiter geführt und koppelt HF ab
- Induktivität muss für den Strom passend gewählt sein
A: Zur Trennung der Gleichspannung vom Empfängereingang.
B: Zur Verbesserung des Tiefpass-Verhaltens.
C: Zur HF-Trennung von RX und LNA.
D: Zur Siebung der Gleichspannung.
A: Strombelastbarkeit
B: Güte
C: Spannungsfestigkeit
D: Temperaturkoeffizient