Strom, Spannung, Widerstand, Leistung, Energie
Navigationshilfe
Diese Navigationshilfe zeigt die ersten Schritte zur Verwendung der Präsentation. Sie kann mit ⟶ (Pfeiltaste rechts) übersprungen werden.
Navigation
Zwischen den Folien und Abschnitten kann man mittels der Pfeiltasten hin- und herspringen, dazu kann man auch die Pfeiltasten am Computer nutzen.

- Pfeil runter und hoch: Nächste / Vorherige Folie
- Pfeil rechts und links: Nächster / Vorheriger Abschnitt
- Leertaste oder „n“: Der Reihe nach alle Elemente in Folien aufdecken oder zur nächsten Folie blättern
- Shift-Leertaste oder „p“: Der Reihe nach Elemente rückwärts zudecken oder zur vorherigen Folie blättern
Weitere Funktionen
Mit ein paar Tastenkürzeln können weitere Funktionen aufgerufen werden. Die wichtigsten sind:
- F1
- Help / Hilfe
- o
- Overview / Übersicht aller Folien
- s
- Speaker View / Referentenansicht
- f
- Full Screen / Vollbildmodus
- b
- Break, Black, Pause / Ausblenden der Präsentation
- Alt-Click
- In die Folie hin- oder herauszoomen
Übersicht
Die Präsentation ist zweidimensional aufgebaut. Dadurch sind in Spalten die einzelnen Abschnitte eines Kapitels und in den Reihen die Folien zu den Abschnitten.
Tippt man ein „o“ ein, bekommt man eine Übersicht über alle Folien des jeweiligen Kapitels. Das hilft sich zunächst einen Überblick zu verschaffen oder sich zu orientieren, wenn man das Gefühlt hat sich „verlaufen“ zu haben. Die Navigation erfolgt über die Pfeiltasten.

Durch Anklicken einer Folie wird diese präsentiert.
Referentenansicht
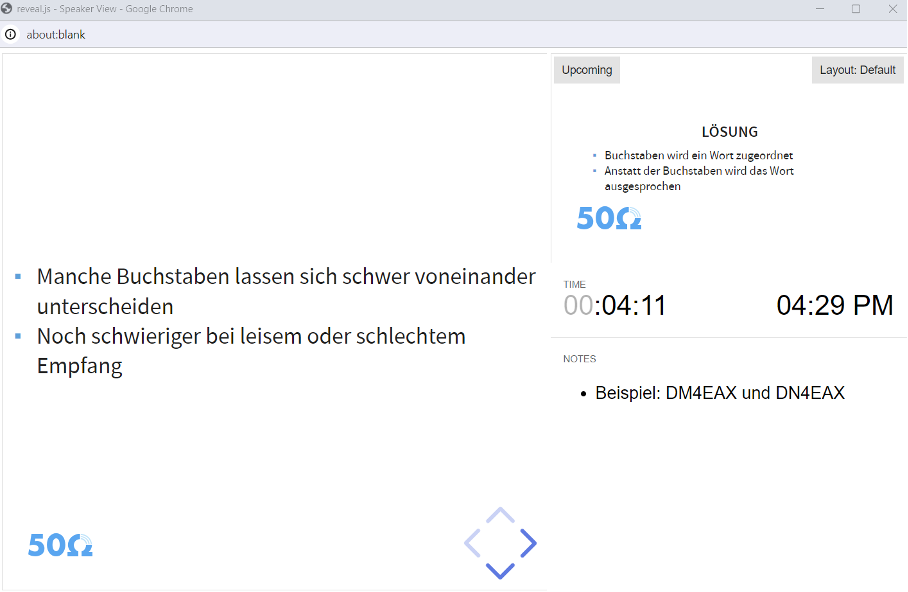
Tippt man ein „s“ ein, bekommt man ein neues Fenster, die Referentenansicht.
Indem man „Layout“ auswählt, kann man zwischen verschieden Anordnungen der Elemente auswählen.
Die Referentenansicht bietet folgende Elemente:
- Links sieht man die aktuelle Folie
- Rechts oben sieht man die nächste Folie
- Rechts in der Mitte Hilfsmittel zur Zeiteinteilung
- Rechts unten, die „Notizen für den Vortragenden“
- Unten die Pfeile zur Navigation
Praxistipps zur Referentenansicht
- Wenn man mit einem Projektor arbeitet, stellt man im Betriebssystem die Nutzung von 2 Monitoren ein: Die Referentenansicht wird dann zum Beispiel auf dem Laptop angezeigt, während die Teilnehmer die Präsentation angezeigt bekommen.
- Bei einer Online-Präsentation, wie beispielsweise auf TREFF.darc.de präsentiert man den Browser-Tab und navigiert im „Speaker View“ Fenster.
- Die Referentenansicht bezieht sich immer auf ein Kapitel. Am Ende des Kapitels muss sie geschlossen werden, um im neuen Kapitel eine neue Referentenansicht zu öffnen.
- Um mit dem Mauszeiger etwas zu markieren oder den Zoom zu verwenden, muss mit der Maus auf den Bildschirm mit der Präsentation gewechselt werden.
Vollbild
Tippt man ein „f“ ein, wird die aktuelle Folie im Vollbild angezeigt. Mit „Esc“ kann man diesen wieder verlassen.
Das ist insbesondere für den Bildschirm mit der Präsentation für das Publikum praktisch.
Ausblenden
Tippt man ein „b“ ein, wird die Präsentation ausgeblendet.
Sie kann wie folgt wieder eingeblendet werden:
- Durch klicken in das Fenster.
- Durch nochmaliges Drücken von „b“.
- Durch klicken der Schaltfläche „Resume presentation:

Zoom
Bei gedrückter Alt-Taste und einem Mausklick in der Präsentation wird in diesen Teil hineingezoomt. Das ist praktisch, um Details von Schaltungen hervorzuheben. Durch einen nochmaligen Mausklick zusammen mit Alt wird wieder herausgezoomt.
Das Zoomen funktioniert nur im ausgewählten Fenster. Die Referentenansicht ist hier nicht mit dem Präsenationsansicht gesynct.
Physikalische Stromrichtung
- Technische Stromrichtung vom Plus-Pol zum Minus-Pol
- In der Wissenschaft hat sich später erst herausgestellt, dass sich in Metallen die negativ geladenen Teilchen (Elektronen) bewegen
- Elektronen werden vom Minus-Pol der Spannungsquelle abgestoßen und vom Plus-Pol angezogen
- Die Physikalische Stromrichtung ist entgegen gesetzt zur technischen Stromrichtung
Strom- und Spannungsmessung II
- Der Strom wird im Stromkreis eingeschleift gemessen
- Die Spannung wird über den Widerstand gemessen
- Der Widerstand im Voltmeter soll hochohmig sein → Strom nimmt den Weg des geringsten Widerstandes
A: in den Stromkreis einzuschleifen und sollte hochohmig sein.
B: parallel zum Messobjekt anzuschließen und sollte niederohmig sein.
C: parallel zum Messobjekt anzuschließen und sollte hochohmig sein.
D: in den Stromkreis einzuschleifen und sollte niederohmig sein.
Strom- und Spannungsmessung III
Strom- und Spannungsmessung
- Spannung wird parallel zum Bauteil gemessen
- Strom wird in Reihe mit dem Bauteil gemessen
A: Spannungsmessgerät bei 3, Strommessgerät bei 4.
B: Spannungsmessgerät bei 1, Strommessgerät bei 2.
C: Spannungsmessgerät bei 3, Strommessgerät bei 1.
D: Spannungsmessgerät bei 1, Strommessgerät bei 3.
A: 2, 4 und 1
B: 1, 2 und 3
C: 1, 3 und 4
D: 2, 3 und 4
Messgenauigkeit
Der angezeigte Messwert unterscheidet sich meist vom tatsächlichen Wert
- Innenwiderstand des Messgeräts
- Auflösungsvermögen → kleinste Auflösung
- Anzeige verändert sich erst nach Änderung um die kleinste Auflösung
- Hersteller ermittelt die Abweichung
- Abweichung wird im Datenblatt angegeben
A: 9,75 % zu niedrig bestimmen.
B: 5 % zu niedrig bestimmen.
C: 10,25 % zu hoch bestimmen.
D: 5 % zu hoch bestimmen.
Lösungsweg
- Prozentrechnung – die absoluten Werte sind nicht relevant
- gegeben: $U_{\textrm{Abw}}$ mit
95 % vom Realwert - gegeben: $I_{\textrm{Abw}}$ mit
95 % vom Realwert - gesucht: Abweichung der Leistung $P = U \cdot I$
$$\begin{equation}\begin{split} \nonumber P_{\textrm{Abw}} &= 100\% – (U_{\textrm{Abw}} \cdot I_{\textrm{Abw}})\\ &= 100\% – (95\% \cdot 95\%)\\ &= 100\% – 90,25\%\\ &= 9,75\% \end{split}\end{equation}$$
Strom durch Multimeter
- Auch bei einer Spannungsmessung fließt ein Strom durch ein Messegerät
- Es findet eine Stromteilung statt
- Durch den hohen Innenwiderstand ist der abfließende Strom verhältnismäßig klein
A:
B:
C:
D:
Lösungsweg
- gegeben: $U = 0,5V$
- gegeben: $R = 10M\Omega$
- gesucht: $I$
$$\begin{equation} \nonumber I = \frac{U}{R} = \frac{0,5V}{10M\Omega} = 50nA \end{equation}$$
Thermoumformer
- Messgerät, bei dem die abgestrahlte Wärme an einem Widerstand gemessen wird
- Aus der abgestrahlten Wärme wird mit einem Thermoelement eine Gleichspannung erzeugt, die gemessen werden kann
- Wird dann eingesetzt, wenn eine elektrische Messung nicht möglich ist, z.B. bei nicht-periodischen Signalen
- Es wird der Effektivwert der Stromstärke gemessen
A: ein Messgerät mit Thermoumformer.
B: ein Digitalmultimeter.
C: ein Oszillograf.
D: ein Messgerät mit Diodentastkopf.
Zeigerinstrumente ablesen
- Richtige Auswahl der zu messenden Größe mit dem Schalter wählen
- Richtige Skala anhand des Messbereichs wählen
- Ggf. muss um einen Faktor 10 oder 100 multipliziert oder dividiert werden
- Vorteil: Man sieht kontinuierliche Änderungen

Parallaxenfehler
- Parallaxenfehler vermeiden, indem gerade drauf geschaut wird
- Viele Zeigerinstrumente haben einen Spiegel hinter dem Zeiger
- Wenn der Zeiger sich im Spiegelbild überdeckt, wird gerade drauf geschaut

A:
B:
C:
D:
A:
B:
C:
D:
Spitzen- und Effektivwert
Spitzenwert
- Der Spitzenwert einer Sinusschwingung entspricht der Amplitude
- Von Nulllinie bis höchstem Wert
- Spitzen-Spitzen-Wert von niedrigstem bis höchstem Wert
Spitzen-Spitzen-Wert bei sinusförmigen Spannungen
$U_{SS} = 2\cdot \^{U}$
A:
B:
C:
D:
A:
B:
C:
D:
Effektivwert
Bei einer Wechselspannung der Wert, der in einem Widerstand zu einer vergleichsweisen Gleichspannung in Leistung umgesetzt wird
Bei Spannungen (ohne Herleitung)
$\^{U} = U_{eff}\cdot \sqrt{2}$
A:
B:
C:
D:
Lösungsweg
$\^{U} = U_{eff}\cdot \sqrt{2}$
$U_{eff} = \dfrac{\^{U}}{\sqrt{2}}$
$U_{eff} = \dfrac{1V}{1,41} \approx 0,7V$
A:
B:
C:
D:
Lösungsweg
$\^{U} = U_{eff}\cdot \sqrt{2}$
$U_{eff} = \dfrac{\^{U}}{\sqrt{2}}$
$U_{eff} = \dfrac{12V}{1,41} \approx 8,5V$
A:
B:
C:
D:
Lösungsweg
$\^{U} = U_{eff}\cdot \sqrt{2}$
$\^{U} = 12V\cdot 1,41 \approx 17V$
$U_{SS} = 2\cdot \^{U}$
$U_{SS} = 2\cdot 17V = 34V$
A:
B:
C:
D:
Lösungsweg
$\^{U} = U_{eff}\cdot \sqrt{2}$
$\^{U} = 230V\cdot 1,41 \approx 325V$
A:
B:
C:
D:
Oszilloskop I
Periode
- Dauer einer vollständigen Schwingung
- Wird zur Ermittlung der Frequenz benötigt, z.B. Oszilloskop
- Periode steht im umgekehrten Verhältnis zur Frequenz
- Formelzeichen T, Einheit Sekunde (s)
$T = \dfrac{1}{f} \Rightarrow f = \dfrac{1}{T}$
Hier gibt es die Möglichkeit das Ganze nochmal auszuprobieren. An den Reglern kann man die Amplitude $a$ und die Periode $T$ einer Sinusschwingung einstellen.
| Amplitude: |
$a$= 50%
|
|
| Periode: |
$T$= 1s und $f$=1Hz
|
A:
B:
C:
D:
Periodendauer ablesen
- Kästchen einer ganzen Periode im Nulldurchgang zählen
- Mit der Zeiteinheit multiplizieren
- Bei 8 Kästchen und
2 ms pro Kästchen → 8 ×2 ms =16 ms
A:
B:
C:
D:
Frequenz ermitteln
$f = \dfrac{1}{T}$
Erst Periodendauer ermitteln, dann Frequenz ausrechnen
A:
B:
C:
D:
Lösungsweg
Eine Periode ist 4 Kästchen lang
$T = 4\cdot 5ms = 20ms$
$f = \dfrac{1}{T} = \dfrac{1}{20\cdot10^{-3}s} = $
$0,05\frac{1}{10^{-3}s} = 0,05\cdot10^3Hz = 0,05kHz = 50Hz$
A:
B:
C:
D:
A:
B:
C:
D:
Lösungsweg
Eine Periode ist 4 Kästchen lang
$T = 4\cdot 3\mu s = 12\mu s$
$f = \dfrac{1}{T} = \dfrac{1}{12\cdot10^{-6}s} = $
$0,0833\frac{1}{10^{-6}s} = 0,0833\cdot10^6Hz = 0,0833MHz = 83,3kHz$
A:
B:
C:
D:
Impuls
- Ein Signal springt von einem Wert auf einen höheren und zu einem späteren Zeitpunkt zurück
- Dauer des Impulses wird von Mitte der ansteigenden Flanke bis zur Mitte der abfallenden Flanke gemessen
A:
B:
C:
D:
NF-Verzerrungen
- Manchmal werden Signale ungewollt verformt.
- Das geschieht zum Beispiel, wenn in einen Verstärker eine zu hohe Eingangsspannung eingespeist wird.
- Man sagt dann, der Verstärker ist übersteuert und sein Ausgangssignal verzerrt.
- Das kann mit einem Oszilloskop sichtbar gemacht werden.
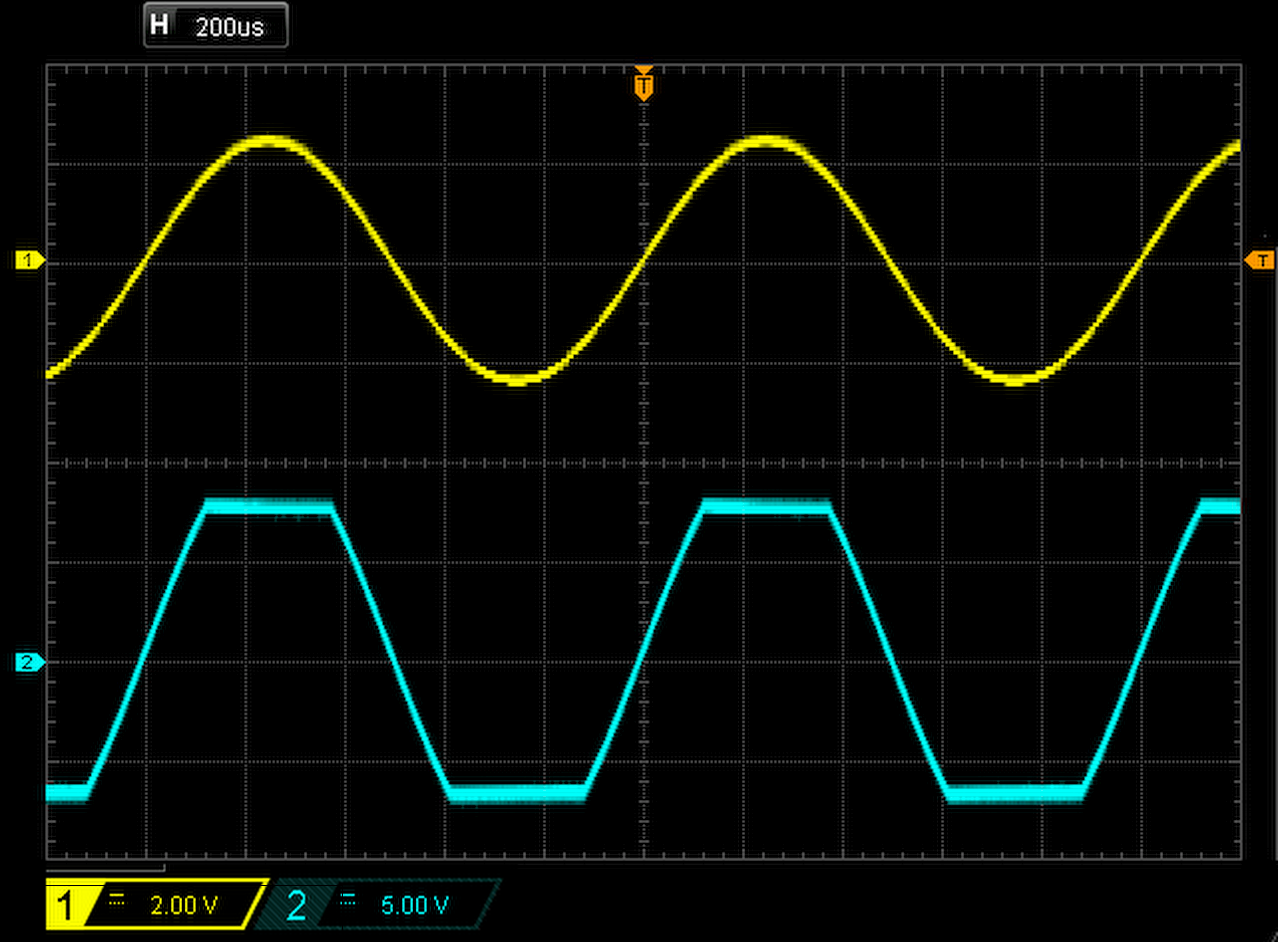
A: Ein Frequenzzähler
B: Ein Transistorvoltmeter
C: Ein Vielfachmessgerät
D: Ein Oszilloskop
Oszilloskop II
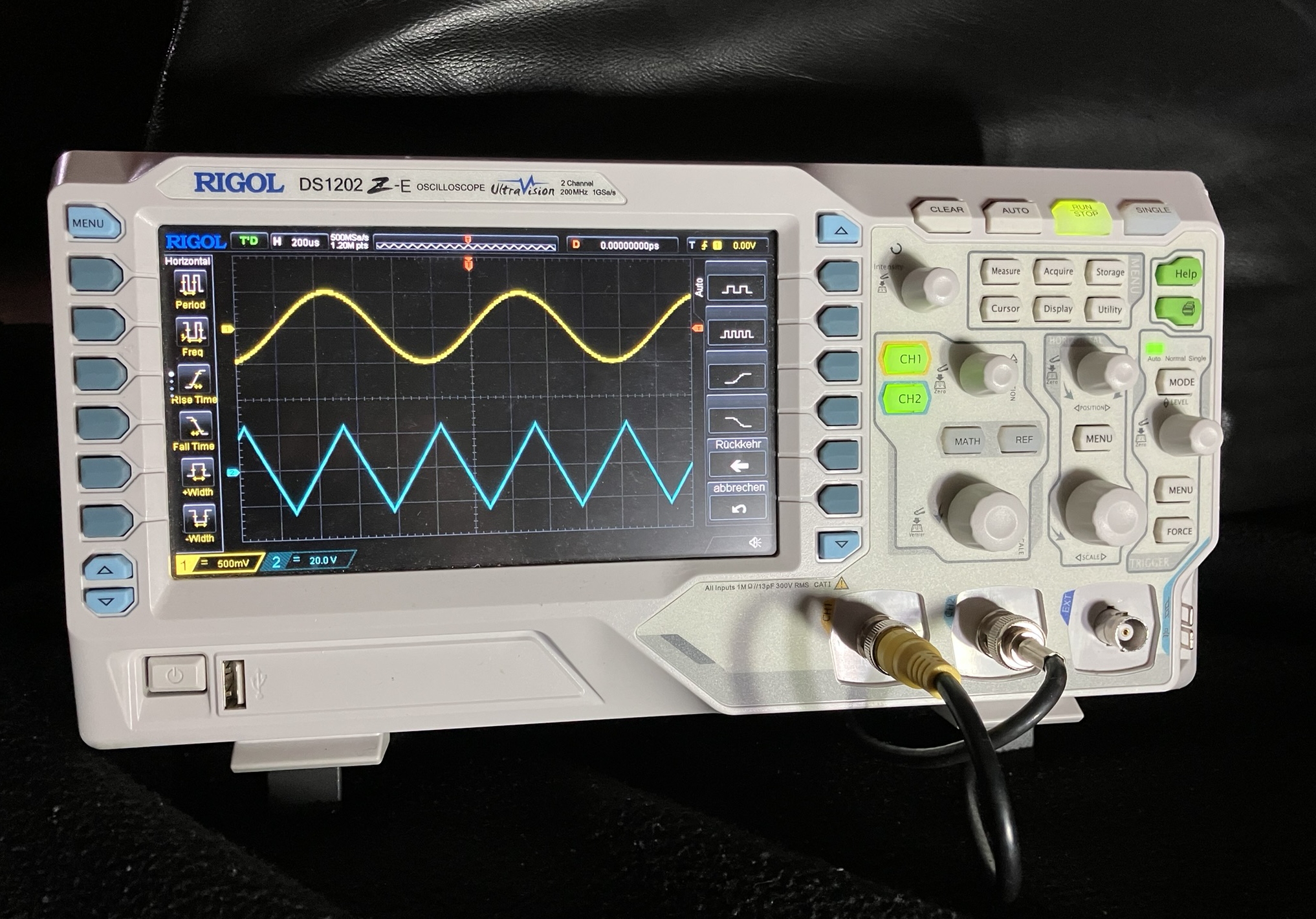
- Zeigt den zeitlichen Verlauf von Spannungen dar
- Misst die Signalform
A: Absorptionsfrequenzmesser
B: Frequenzzähler
C: Dipmeter
D: Oszilloskop
A: hochohmigen Vielfachinstrument in Stellung AC.
B: breitbandigen Detektor und Kopfhörer.
C: empfindlichen SWR-Meter in Stellung Wellenmessung.
D: breitbandigen Oszilloskop.
Pulsbreite
Definition: Die Pulsbreite liegt bei
A: 90 % des Spitzenwertes gemessen.
B: 70 % des Spitzenwertes gemessen.
C: 10 % des Spitzenwertes gemessen.
D: 50 % des Spitzenwertes gemessen.
Trigger
- Trigger wertet das anliegende Signal aus
- Z.B. die Spannung 0 von negativ nach positiv durchlaufen
- Dadurch kann bei einer Welle ein stehendes Bild gezeigt werden
A: Triggereinrichtung
B: Y-Vorteiler
C: Frequenzmarken-Generator
D: X-Vorteiler
Tastköpfe

- Zur Messung der Spannung
- Spitze als Haken oder Nadel gebaut
- Bezugsmasse meistens über eine separate Krokodilklemme
- 10:1-Tastköpfe teilen die Spannung auf ein Zehntel
Messung mit einem Oszilloskop

A:
B:
C:
D:
Lösungsweg
- gegeben: $R=50\Omega$
- gegeben: (aus Darstellung) $\^{U} = 100V$
- gesucht: $P_{\textrm{PEP}}$
$$\begin{equation}\begin{split} \nonumber P_{\textrm{PEP}} &= \frac{U_{\textrm{eff}}^2}{R} = \frac{(\frac{100V}{\sqrt{2}})^2}{50\Omega}\\ &=\frac{\frac{(100V)^2}{2}}{50\Omega} = \frac{5000V^2}{50\Omega} = 100W \end{split}\end{equation}$$
A:
B:
C:
D:
Lösungsweg
- gegeben: $R=50\Omega$
- gegeben: (aus Darstellung mit 10:1-Tastkopf) $\^{U} = 6V\cdot 10$
- gesucht: $P_{\textrm{PEP}}$
$$\begin{equation}\begin{split} \nonumber P_{\textrm{PEP}} &= \frac{U_{\textrm{eff}}^2}{R} = \frac{(\frac{6V\cdot 10}{\sqrt{2}})^2}{50\Omega}\\ &=\frac{\frac{(60V)^2}{2}}{50\Omega} = 36W \end{split}\end{equation}$$
SMD-Widerstände
- SMD: Surface Mounted Device
- Widerstand in sehr kleiner Bauform
- Letzte Stelle des aufgedruckten Widerstandswerts gibt die Zehnerpotenz an
A: Auf dem Widerstand ist der Wert in Form von Farbringen aufgedruckt, wobei der letzte Farbring die Zehnerpotenz angibt.
B: Auf dem Widerstand ist der Wert in Form von Zahlen abgedruckt, wobei die angegebene Zahl dem Wert des Widerstands entspricht.
C: Auf dem Widerstand ist der Wert in Form von Farbringen aufgedruckt, wobei der letzte Farbring die Toleranz angibt.
D: Auf dem Widerstand ist der Wert in Form von Zahlen abgedruckt, wobei die letzte Ziffer die Zehnerpotenz angibt.
A:
B:
C:
D:
A:
B:
C:
D:
A:
B:
C:
D:
Leiterwiderstand
Widerstand von Drähten
- Leitfähiges Material besteht aus Atomen in einer (Gitter-)Struktur
- Elektronen werden geteilt und sind dadurch frei beweglich
- Je nach Material gibt es mehr oder weniger freie Elektronen, die auf Atome stoßen
Spezifischer Widerstand $\rho$
$R = \frac{\rho\cdot l}{A_{\textrm{Dr}}}$
- $l$: Drahtlänge
- $A_{\textrm{Dr}}$: Drahtquerschnitt
- $\rho$: Spezifischer Widerstand in Ωmm2/m
Kupfer: 0,018
Aluminium: 0,028
Gold: 0,022
Silber: 0,016
Zink: 0,11
Eisen: 0,1
Messing: 0,07
A:
B:
C:
D:
Lösungsweg
- gegeben: $l = 1,8m$
- gegeben: $d = 0,2mm$
- gegeben: $\rho = 0,018 \frac{\Omega mm^2}{m}$
- gesucht: $R$
$$\begin{equation} \nonumber A_{\textrm{Dr}} = \frac{d^2\cdot \pi}{4} = \frac{(0,2mm)^2 \cdot \pi}{4} = \frac{\pi}{100}mm^2 = 0,0314mm^2 \end{equation}$$
$$\begin{equation} \nonumber R = \frac{\rho\cdot l}{A_{\textrm{Dr}}} = \frac{0,018 \frac{\Omega mm^2}{m} \cdot 1,8m}{0,0314mm^2} \approx 1,02\Omega \end{equation}$$
A:
B:
C:
D:
Lösungsweg
- gegeben: $A_{\textrm{Dr}} = 0,5mm^2$
- gegeben: $R = 1,5\Omega$
- gegeben: $\rho = 0,018 \frac{\Omega mm^2}{m}$
- gesucht: $l$
$$\begin{equation}\begin{align} \nonumber R &= \frac{\rho\cdot l}{A_{\textrm{Dr}}}\\ \nonumber \Rightarrow l &= \frac{R\cdot A_{\textrm{Dr}}}{\rho} = \frac{1,5\Omega \cdot 0,5mm^2}{0,018 \frac{\Omega mm^2}{m}} \approx 41,7m \end{align}\end{equation}$$
Temperaturkoeffizient
- Widerstand von Metallen steigt bei zunehemender Temperatur
- Atome bewegen sich bei höherer Temperatur mehr, wodurch es zu mehr Kollisionen mit Elektronen kommt
A: Der Widerstand sinkt mit zunehmender Temperatur, d. h. der Temperaturkoeffizient ist negativ.
B: Der Widerstand ändert sich nicht mit zunehmender Temperatur, d. h. der Temperaturkoeffizient ist Null.
C: Der Widerstand oszilliert mit zunehmender Temperatur, d. h. der Temperaturkoeffizient ist komplex.
D: Der Widerstand steigt mit zunehmender Temperatur, d. h. der Temperaturkoeffizient ist positiv.
Widerstandsmaterialien
Drahtwiderstände
- Draht aus einem Leiter mit gutem konstanten Widerstand trotz ändernder Temperatur
- Dadurch ist eine hohe Last möglich
- Oftmals gewickelt für mehr Länge
- Dadurch nur für niedrige Frequenzen geeignet
A: Drahtwiderstände
B: LDR-Widerstände
C: Metallschichtwiderstände
D: Metalloxidschichtwiderstände
Metallschichtwiderstand
- Widerstandsmaterial als dünne Schicht auf einem Träger
- Hohe Widerstandswerte möglich
- Sehr präzise
- Geringe Temperaturabhängigkeit
A: Metalloxidschichtwiderstände
B: LDR-Widerstände
C: Drahtwiderstände
D: Metallschichtwiderstände
Metalloxidschichtwiderstand
- Ähnlich wie Metallschichtwiderstand
- Induktionsarm
- Für hohe Frequenzen geeignet
A: Drahtwiderstände
B: Metalloxidschichtwiderstände
C: LDR-Widerstände
D: Metallschichtwiderstände
A: hohen elektrischen und elektronischen Leitwert
B: hohe Eigeninduktivität und Eigenkapazität
C: geringe Eigeninduktivität und Eigenkapazität
D: geringen elektrischen und elektronischen Leitwert
Widerstandstoleranzen
- Einfache Prozentrechnung
- Korrektur nach unten und oben vom angegebenen Widerstandswert
A: 4,7 bis
B: 5040 bis
C: 4760 bis
D: 5,2 bis
A: 4760 bis
B: 5040 bis
C: 5240 bis
D: 4760 bis
Heißleiter und Kaltleiter
Heißleiter
- Heißleiter ist ein temperaturabhängiger Widerstand
- Englisch: Negative Temperature Coefficient Thermistor (NTC)
- Leitet bei hohen Temperaturen elektrischen Strom besser
A: LDR
B: NTC
C: VDR
D: PTC
Kaltleiter
- Kaltleiter ist ein temperaturabhängiger Widerstand
- Englisch: Positive Temperature Coefficient Thermistor (PTC)
- Leitet bei tiefen Temperaturen elektrischen Strom besser
Leistung beim Wechselstrom
Berechnung mit Effektivwerten
$U_{\textrm{eff}} = \frac{\^{U}}{\sqrt{2}}$
$I_{\textrm{eff}} = \frac{\^{I}}{\sqrt{2}}$
$P = U_{\textrm{eff}} \cdot I_{\textrm{eff}}$
A:
B:
C:
D:
Lösungsweg
- gegeben: $I_{\textrm{max}} = 0,5A$
- gegeben: $R = 20\Omega$
- gesucht: $P$
$$\begin{equation}\begin{split} \nonumber P &= I^2 \cdot R = (\frac{I_{\textrm{max}}}{\sqrt{2}})^2 \cdot R\\ &= \frac{(0,5A)^2}{2} \cdot 20\Omega \\ &= \frac{1}{8}A^2 \cdot 20\Omega = 2,5W \end{split}\end{equation}$$
Leistung II
Leistungsberechnung
Wir kennen bereits
$P = U\cdot I = \dfrac{U^2}{R} = I^2\cdot R$
Nach U umgestellt:
$U = \dfrac{P}{I} = \sqrt{P \cdot R}$
Nach I umgestellt:
$I = \dfrac{P}{U} = \sqrt{\dfrac{P}{R}}$
A: $I = \sqrt{P\cdot R}; U = \sqrt{\dfrac{P}{R}}$
B: $I = \sqrt{\dfrac{P}{R}}; U = \sqrt{P\cdot R}$
C: $I = \dfrac{\sqrt{P}}{R}; U = \sqrt{P}\cdot R$
D: $I = \sqrt{\dfrac{R}{P}}; U = \sqrt{P\cdot R}$
A: $R = \dfrac{U^2}{P}; R = P\cdot I^2$
B: $R = \dfrac{U^2}{P}; R = \dfrac{P}{I^2}$
C: $R = U^2\cdot I; R = \dfrac{P}{I^2}$
D: $R = \dfrac{P}{U^2}; R = P\cdot I^2$
A: $U = R\cdot P$
B: $U = \dfrac{P}{R}$
C: $U = \sqrt{P\cdot R}$
D: $U = \sqrt{\dfrac{P}{R}}$
A:
B:
C:
D:
A:
B:
C:
D:
A:
B:
C:
D:
A:
B:
C:
D:
A:
B:
C:
D:
A:
B:
C:
D:
Leistung bei Wechselspannung
- Bei Wechselspannungen muss mit dem Effektivwert gerechnet werden
A: Nein, da die Blindleistung nicht berücksichtigt wird.
B: Ja, wenn mit den Spitzenwerten gerechnet wird.
C: Nein, da die periodische Änderung von Strom und Spannung dann vernachlässigt wird.
D: Ja, wenn mit den Effektivwerten gerechnet wird.
A:
B:
C:
D:
PEP
- Peak Envelope Power ist die Spitzenleistung eines Senders
- Leistung bei der höchsten Spitze einer Hochfrequenzschwingung
A: die durchschnittliche Leistung, die ein Sender unter normalen Betriebsbedingungen an die Antennenspeiseleitung während eines Zeitintervalls abgibt, das im Verhältnis zur Periode der tiefsten Modulationsfrequenz ausreichend lang ist.
B: die unmittelbar nach dem Senderausgang messbare Leistung über die Spitzen der Periode einer durchschnittlichen Hochfrequenzschwingung, bevor Zusatzgeräte (z. B. Anpassgeräte) durchlaufen werden.
C: die Leistung, die der Sender unter normalen Betriebsbedingungen während einer Periode der Hochfrequenzschwingung bei der höchsten Spitze der Modulationshüllkurve durchschnittlich an einen reellen Abschlusswiderstand abgeben kann.
D: das Produkt aus der Leistung, die unmittelbar der Antenne zugeführt wird, und ihrem Gewinnfaktor in einer Richtung, bezogen auf den Halbwellendipol.
Mittlere Leistung
- Durchschnittliche Leistung eines Senders
- Beschreibung ergibt zu einem späteren Zeitpunkt mehr Sinn, wenn Hüllkurven durchgesprochen wurden
A: die durchschnittliche Leistung, die ein Sender unter normalen Betriebsbedingungen an die Antennenspeiseleitung während eines Zeitintervalls abgibt, das im Verhältnis zur Periode der tiefsten Modulationsfrequenz ausreichend lang ist.
B: die unmittelbar nach dem Senderausgang messbare Leistung über die Spitzen der Periode einer durchschnittlichen Hochfrequenzschwingung, bevor Zusatzgeräte (z. B. Anpassgeräte) durchlaufen werden.
C: die durchschnittliche Leistung, die ein Sender unter normalen Betriebsbedingungen während einer Periode der Hochfrequenzschwingung bei der höchsten Spitze der Modulationshüllkurve der Antennenspeiseleitung zuführt.
D: das Produkt aus der Leistung, die unmittelbar der Antenne zugeführt wird, und ihrem Gewinnfaktor in einer Richtung, bezogen auf den Halbwellendipol.
Dezibel I
Dezibel einfach erklärt
| Was | Leistung in mW |
|---|---|
| effektive Leistung EME-Station | 100 000 000 |
| Standard Transceiver | 100 000 |
| Kleine Handfunke | 1 000 |
| Lautsprechersignal (Zimmerlautstärke) | 100 |
| Kopfhörersignal | 1 |
| Lautes KW-Signal | 0,000 001 |
| Leises KW-Signal (Antenneneingang RX) | 0,000 000 000 001 |
Wer mit diesen Zahlen umgeht, fängt automatisch an, die Nullen zu zählen.
Wir zählen die Nullen (und nennen das Ergebnis „Bel“)
| Was | Leistung in mW | Bel |
|---|---|---|
| effektive Leistung EME-Station | 100 000 000 | 8 |
| Standard Transceiver | 100 000 | 5 |
| Kleine Handfunke | 1 000 | 3 |
| Lautsprechersignal (Zimmerlautstärke) | 100 | 2 |
| Kopfhörersignal | 1 | 0 |
| Lautes KW-Signal | 0,000 001 | -6 |
| Leises KW-Signal (Antenneneingang RX) | 0,000 000 000 001 | -12 |
dBm = Dezibel bezogen auf mW
| Was | Leistung in mW | Bel | dBm |
|---|---|---|---|
| effektive Leistung EME-Station | 100 000 000 | 8 | 80 |
| Standard Transceiver | 100 000 | 5 | 50 |
| Kleine Handfunke | 1 000 | 3 | 30 |
| Lautsprechersignal (Zimmerlautstärke) | 100 | 2 | 20 |
| Kopfhörersignal | 1 | 0 | 0 |
| Lautes KW-Signal | 0,000 001 | -6 | -60 |
| Leises KW-Signal (Antenneneingang RX) | 0,000 000 000 001 | -12 | -120 |
Leistungsverstärkung
Empfänger
- Eingangssignal: 0,000 000 000
001 mW - Ausgangssignal:
100 mW - Benötigte Verstärkung: 100 000 000 000 000
Sender
- Frequenzerzeugende Stufe (Oszillator):
10 mW - Ausgangssignal: 100
000 mW - Benötigte Verstärkung: 10 000
Leistungsverstärkung mit dB
Empfänger
- Eingangssignal: 0,000 000 000
001 mW = -120 dBm - Ausgangssignal:
100 mW =20 dBm - Benötigte Verstärkung: 100 000 000 000 000 =
140 dB
Sender
- Frequenzerzeugende Stufe (Oszillator):
10 mW =10 dBm - Ausgangssignal: 100
000 mW =50 dBm - Benötigte Verstärkung: 10 000 =
40 dB
Wichtige Leistungsfaktoren
| dB | ≈ Leistungsfaktor |
|---|---|
| 0 | 1 |
| 1,5 | $\sqrt{2} = 1,41$ |
| 2,15 | 1,64 |
| 3 | 2 |
| 5 | $\sqrt{10} = 3,16$ |
| 6 | 4 |
| 10 | 10 |
| 20 | 100 |
Berechnung mit Taschenrechner
Ältere Modelle
- Faktor-Wert → log-Taste → ×10 → dB
- dB-Wert → ÷10 → 10x-Taste → Faktor
Neuere Modelle
- log-Taste → Faktor-Wert → )-Taste → ×10 → =-Taste → dB
- 10x-Taste → dB-Wert → ÷10 → =-Taste → Faktor
A:
B:
C:
D:
Dezibel II
Dezibel
- Logarithmische Angabe von Verhältnissen, insbesondere bei Leistungen
- Macht das Arbeiten mit kleinen und großen Leistungen einfacher
- Verstärkungen und Dämpfungen lassen sich einfacher berechnen
Leistungspegel
Faktor 10
Leistung bezogen auf
$p = 10\cdot \log_{10}(\frac{P}{1mW})\textrm{dBm}$
→ $0\textrm{dBm}$ liegt bei $P = 1mW$ vor
Leistung bezogen auf
$p = 10\cdot \log_{10}(\frac{P}{1W})\textrm{dBW}$
→ $0\textrm{dBW}$ liegt bei $P = 1W$ vor
A:
B:
C:
D:
A:
B:
C:
D:
Spannungspegel
Faktor 20
$u = 20\cdot \log_{10}(\frac{U}{0,775V})\textrm{dBu}$
Spannung bezogen auf
→ $0\textrm{dBu}$ liegt bei $U = 0,775V$ vor
Spannung bezogen auf
→ $0\textrm{dBV}$ liegt bei $U = 1V$ vor
Spannung bezogen auf 1 µV
→ $0\textrm{dBµV}$ liegt bei $U = 1µV$ vor
A:
B:
C:
D:
Berechnungen
A: $10^1$ W.
B: $10^{0,5}$ W.
C: $10^{20}$ W.
D: $10^2$ W.
Lösungsweg
- gegeben: $p = 20\textrm{dBW}$
- gesucht: $P$
$$\begin{equation}\begin{align} \nonumber p &= 10\cdot \log_{10}(\frac{P}{1W})\textrm{dBW}\\ \nonumber \Rightarrow P &= 10^{\frac{p}{10}} \cdot 1W = 10^{\frac{20\textrm{dBW}}{10}} \cdot 1W = 10^2W \end{align}\end{equation}$$
A:
B:
C:
D:
A:
B:
C:
D:
Lösungsweg
1W = 1000mW
1000mW × 10 = 10000mW = 40dBm
A:
B:
C:
D:
Lösungsweg
- 16dB = 10dB + 6dB = 10 × 4 = 40
- 1W × 40 = 40W
A:
B:
C:
D:
Lösungsweg
- gegeben: $u = 120\textrm{dBµV}/m$
- gesucht: $U$
$$\begin{equation}\begin{align} \nonumber u &= 20\cdot \log_{10}(\frac{U}{1\textrm{µV}})\textrm{\textrm{dBµV}}\\ \nonumber \Rightarrow U &= 10^{\frac{u}{20}} \cdot 1\textrm{µV} = 10^{\frac{120\textrm{dBµV}/m}{20}} \cdot 1\textrm{µV} = 1V/m \end{align}\end{equation}$$
In der Literatur ist oft zu finden: 120dBµV = 1V
Ladung und Energie
Elektrische Ladung
Strom über Zeit
$Q = I\cdot t$
in Amperesekunde (As)
A: Kilowatt (kW)
B: Amperesekunde (As)
C: Joule (J)
D: Ampere (A)
Elektrische Energie
Leistung über Zeit
$W = P\cdot t$
in Joule (J) auf Sekunde bezogen oder Wattstunden (Wh)
A: Watt (W) bzw. Voltampere (VA)
B: Volt (V) bzw. Watt pro Ampere (W/A)
C: Joule (J) bzw. Wattstunden (Wh)
D: Watt (W) bzw. Joule pro Stunde (J/h)
A:
B:
C:
D:
Lösungweg
- gegeben: $U = 230V$
- gegeben: $I = 0,63A$
- gegeben: $t = 7h$
- gesucht: $W$
$$\begin{equation} \nonumber W = P\cdot t = U\cdot I\cdot t = 230V\cdot 0,63A\cdot 7h = 1,01kWh \end{equation}$$
A:
B:
C:
D:
Lösungsweg
- gegeben: $U = 10V$
- gegeben: $R = 100\Omega$
- gegeben: $t = 1h$
- gesucht: $W$
$$\begin{equation}\begin{split} \nonumber W = P\cdot t = \frac{U^2}{R} \cdot t = \frac{(10V)^2}{100\Omega}\cdot 1h &= 1Wh \cdot 3600s\\ &= 3600J\end{split}\end{equation}$$