Kondensator I (Klasse E)

Ein sehr wichtiges und oft verwendetes Bauteil in der Funktechnik und Elektronik ist der Kondensator.

Man sollte den Aufbau und das Verhalten eines Kondensator gut kennen, damit seine späteren Anwendungen verstanden werden. Wie in Abbildung 39 gezeigt, besteht er aus zwei leitenden Flächen (Platten, Schichten bzw. Elektroden), die durch einen Isolator (Dielektrikum) voneinander getrennt sind. Als Isolatorschicht können unterschiedliche Materialien verwendet werden:

1. Luft beim Luftdrehkondensaotr oder Lufttrimmer
2. Kunststofffolie beim Folienwickelkondensator
3. Keramik für HF-Kondensatoren mit hoher Güte und bei SMD-Kondensatoren
4. Metalloxid beim Elektrolytkondensator.

Die geometrischen Abmessungen bestimmen eine wichtige Eigenschaft eines Kondensators, es ist die Fähigkeit, Ladungen zu speichern. Diese Fähigkeit wird als Kapazität bezeichnet und hierfür wird der Formelbuchstabe $C$ verwendet. Je größer die Kapazität ist, umso mehr elektrische Ladungen $Q$ können gespeichert werden.

$C = \frac{Q}{U}$ mit der Einheit $Q$ in $As$ und $U$ in $V$

$C = \frac{Q}{U}$ mit der Einheit $\dfrac{As}{V}$

Diese Formel steht nicht in der Formelsammlung und wird auch nicht für die Prüfung benötigt.

Statt $\frac{\text{As}}{\text{V}}$ wird die Benennung FARAD zu Ehren des englischen Naturforschers Michael Faraday (1791 – 1867) verwendet.

1 FARAD ist die Kapazität eines Kondensators, in dem eine Ladung von 1 As bei einer Spannung von 1 Volt gespeichert wird.

Wenn die angelegte Spannung erhöht wird, werden mehr Ladungen gespeichert.

Beim Anlegen einer Spannung an einen Kondensator entsteht zwischen den leitenden Platen ein elektrisches Feld E.

Je höher die angelegte Spannung und je kleiner der Abstand zwischen den Platten ist, umso stärker ist das elektrische Feld. Daraus ergibt sich die Formel

$E = \dfrac{U}{d}$

(siehe Formelsammlung Seite 236 unten rechts – Stichwort: Elektrische Feldstärke im homogenen Feld)

Zur Berechnung der Kondensatorkapazität aus den Abmessungen dient folgende Formel:

$C = \frac{\varepsilon_0 \cdot \varepsilon_r \cdot A}{d}$

(siehe Formelsammlung Seite 236 unten rechts – Stichwort: Kapazität eines Kondensators)

$A$ = gegenüberstehende Fläche der leitenden Platten

$d$ = Abstand zwischen den Flächen

$\varepsilon_0 = 0,855 \cdot 10^{-11}\frac{As}{Vm}$: elektrische Feldkonstante

(siehe Formelsammlung Seite 243 unten rechts – Stichwort: elektrische Feldkonstante)

Eine spezielle Eigenschaft des Isolators (Dielektrikum) ist die sogenannte relative Dielektrizitätszahl $\varepsilon_r$ („sprich: Epsilon R“).

Diese Tabelle 2 findet man in der Formelsammlung auf Seite 244.

(siehe Formelsammlung Seite 244 unten – Stichwort: Relative Dielektrizitätszahl)

MERKE:

1. Die Kapazität eines Kondensators sinkt, wenn der Plattenabstand größer wird.
2. Die anliegende Spannung hat keinen Einfluss auf die Kapazität.
3. Eine größere Dielektrizitätszahl erhöht die Kapazität.

Bild zum Elektrolytkondensator folgt

Praktischer Hinweis:

Man kann sich einen Kondensator selber bauen

Schneide zwei Flächen aus ALU-Folie mit den Maßen 5cm x 6cm aus. Zwischen die Flächen legt man dünne Frischhaltefolie und presst oder klebt die Flächen gut zusammen. Diese Konstruktion stellt einen Kondensator dar. Wie groß ist wohl seine Kapazität?

Man kann sie aus den Abmessungen (Fläche, Abstand) und dem Dielektrikum berechnen.

$C = \frac{\varepsilon_0 \cdot \varepsilon_r \cdot A}{d}$

Der gezeigte Selbstbaukondensator hat eine Kapazität von ca. 5339 pF = 5,339 nF.

Mit modernen Messgeräten kann sie auch über den gemessenen Blindwiderstand (z.B. bei 10 MHz) und anschließender Rechnung ermittelt werden.

Siehe Blindwiderstand $Xc$ eines Kondensators in Klasse A

In elektronischen Schaltungen werden sehr unterschiedliche Kondensatorbauformen verwendet:

• Schwingkreiskondensatoren mit hoher Güte (siehe Schwingkreis)
• Koppelkondensatoren in Wechselspannungsverstärkern
• Abblockkondensatoren in Wechselspannungsverstärkern (siehe Abschnitt Verstärker)
• Lade- und Siebkondensatoren in Gleichspannungsnetzteilen (siehe Abschnitt Netzteile)

1. Drehkondensator
2. Lufttrimmer
3. Elektrolytkondensator (kurz: ELKO) 3300 uF
4. Keramikkondennsator in SMD Bauform
5. Folienkondensator
6. Folienkondensator für Wechselspannung 250 V
7. keramischer Rohrkondensator für 7000 V
8. ELKO 47 uF bis 450 V Betriebsspannung
9. keramischer Scheibenkondensator
10. keramischer Trimmkondensator
11. Elektrolytkondensator 2 x 50 uF für 450 V

Je nach Aufbau unterscheidet man:

• Festkondensatoren in Form von Keramikkondensatoren, Folienkondensatoren und Elektrolytkondensatoren
• veränderliche Kondensatoren in Form von Drehkondensatoren und Trimmkondensatoren

Elektrolytkondensatoren (kurz ELKO) enthalten eine dünne, aufgerauhte ALU-Folie, die in einen Elektrolyten (z.B. Borax) eingetaucht ist. Dabei verursacht der Elektrolyt eine chemische Oxidation der Aluminiumoberfläche. Die entstehende Oxidschicht ist sehr dünn und deshalb steigt die Kapazität bei geringer Baugröße sehr stark an. Allerdings hat die dünne Schicht nur eine begrenzte Spannungsfestigkeit, die auf dem ELKO anggeben wird.

Elektrolytkondensatoren dürfen nur an Gleichspannung betrieben werden. Die Polung ist deshalb zu beachten, da sich sonst die Oxidschicht abbaut und somit die Spannungsfestigkeit sinkt. Der Kondesator wird zerstört.

Alle anderen Kondensatoren können auch an Wechselspannung angeschlossen werden.

Kondensatoren verhalten sich unterschiedlich, wenn sie an Gleich- oder Wechselspannung angeschlossen werden.

Messungen mit einem Oszilloskop:

Ein ungeladener Kondensator wird über einen Widerstand an Gleichspannung angeschlossen. Durch die Spannung (Vergleichbar mit einem Druck) werden Ladungen auf die Flächen geschoben, da sich ungleiche Ladungen gegenseitig anziehen. Negative Ladungen = Elektronenüberschuss – Elektronen werden vom negativen Pol der Spannungsquelle auf die angeschlossene leitende Fläche „gedrückt“ Positive Ladungen = Elektronenmangel – Elektronen werden vom positiven Pol der Spannungsquelle „abgesaugt“. Der Kondenator lädt sich auf. Dies geschieht aber nicht schlagartig, sondern zeitlich verzögert und die Spannung am Kondensator steigt dabei nach einer sogenannten „e-Funktion“ an. Die zeitliche Verzögerung hängt vom vorgeschalteten Widerstand ab. Je größer der Widerstand ist, umso länger dauert es, bis der Kondensator „voll“ geladen ist. Das Oszilloskop zeigt diesen Vorgang genau an.

Beim Entladevorgang fließt der Strom entgegen der Ladestromrichtung und die Spannung am Kondensator baut sich langsam ab. Der Verlauf geschieht nach einer speziellen mathematischen Funktion (e-Funktion).

Es gibt auch Simulationsprogramme, die die Spannungs- und Stromänderung beim Lade- und Entladevorgang darstellen können.

EC201: Welchen zeitlichen Verlauf hat die Spannung an einem entladenen Kondensator, wenn dieser über einen Widerstand an eine Gleichspannungsquelle angeschlossen wird?

check

clear

clear

clear

Wenn ein Kondensator hintereinander schnell geladen und entladen wird, dann steigt im Mittel der angezeigte Strom. In der Praxis sieht dies so aus, als ob in einem Stromkreis der Widerstand sinken würde. Deshalb kann man für den Kondensator einen Wechselstromwiderstand angeben.

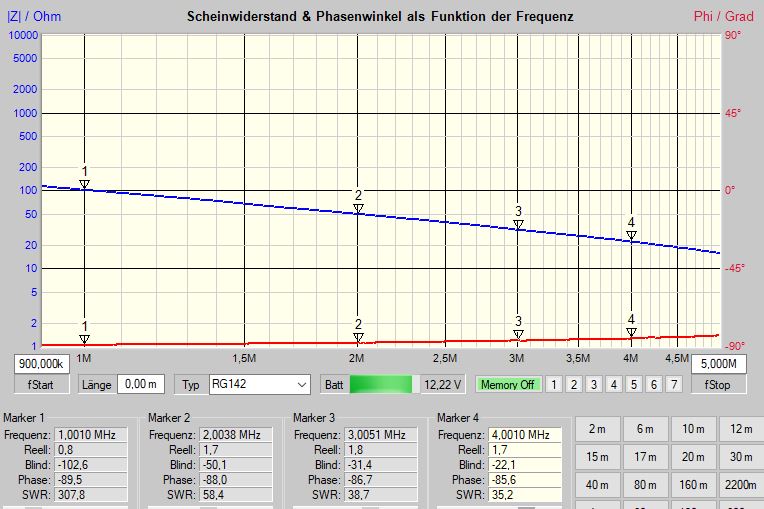
Er wird kapazitiver Blindwiderstand $X_{\textrm{C}}$ genannt.

Wie man aus der folgenden Darstellung eines Antennenanalysators sehen kann sinkt er bei steigender Frequenz .