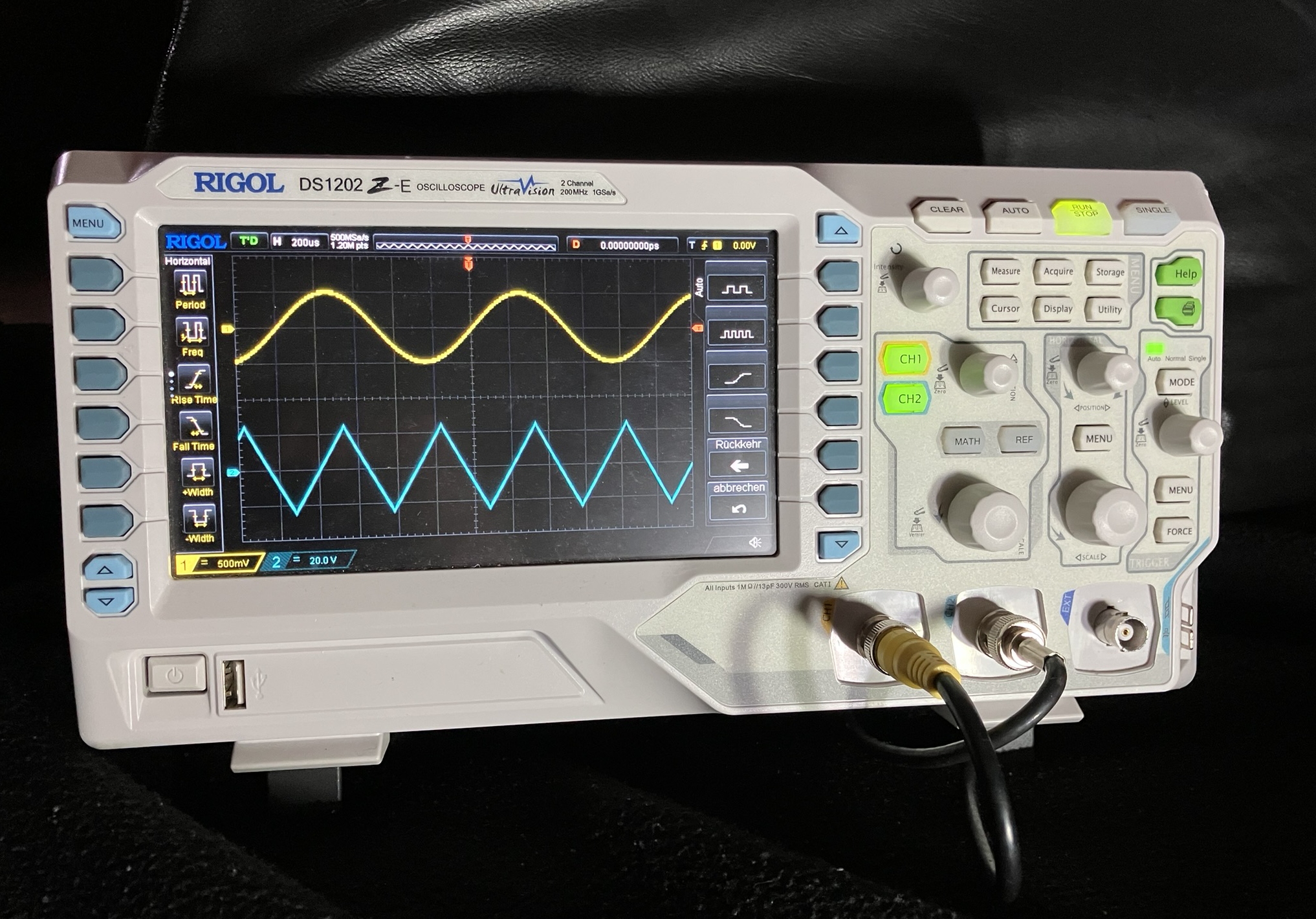
Ein Oszilloskop ist ein Spannungsmessgerät, das den zeitlichen Verlauf von Spannungen visualisieren kann. Genau wie andere Spannungsmessgeräte besitzen Oszilloskope einen hohen Innenwiderstand. Meist lassen sich zwei oder mehr Spannungen gleichzeitig messen. Das Gerät in Abbildung EA-3.6.1 ist beispielsweise so eingestellt, dass sich zwei Signale den Bildschirm teilen.
Betrachten wir die Anzeige des Oszilloskops in Abbildung EA-3.6.2 nun etwas genauer. Mit einem Oszilloskop lassen sich beispielsweise die Kenngrößen einer sinusförmigen Wechselspannung ($T$, $\hat{U}$, $U_\text{SS}$ und $U_\text{eff}$) bestimmen. Neben dem Signalverlauf werden eine Zeit- und eine Spannungsangabe eingeblendet – im Beispiel $\qty{50,0}{\nano\second}$ und $\qty{500}{\milli\volt}$. Das bedeutet, dass ein Kästchen in horizontaler Richtung 50 Nanosekunden und in vertikaler Richtung 500 Millivolt entspricht. Diese Kästchen werden oft als Divisionen oder Skalenteile bezeichnet, daher auch die Schreibweise $\qty{500}{\milli\volt\per div}$.
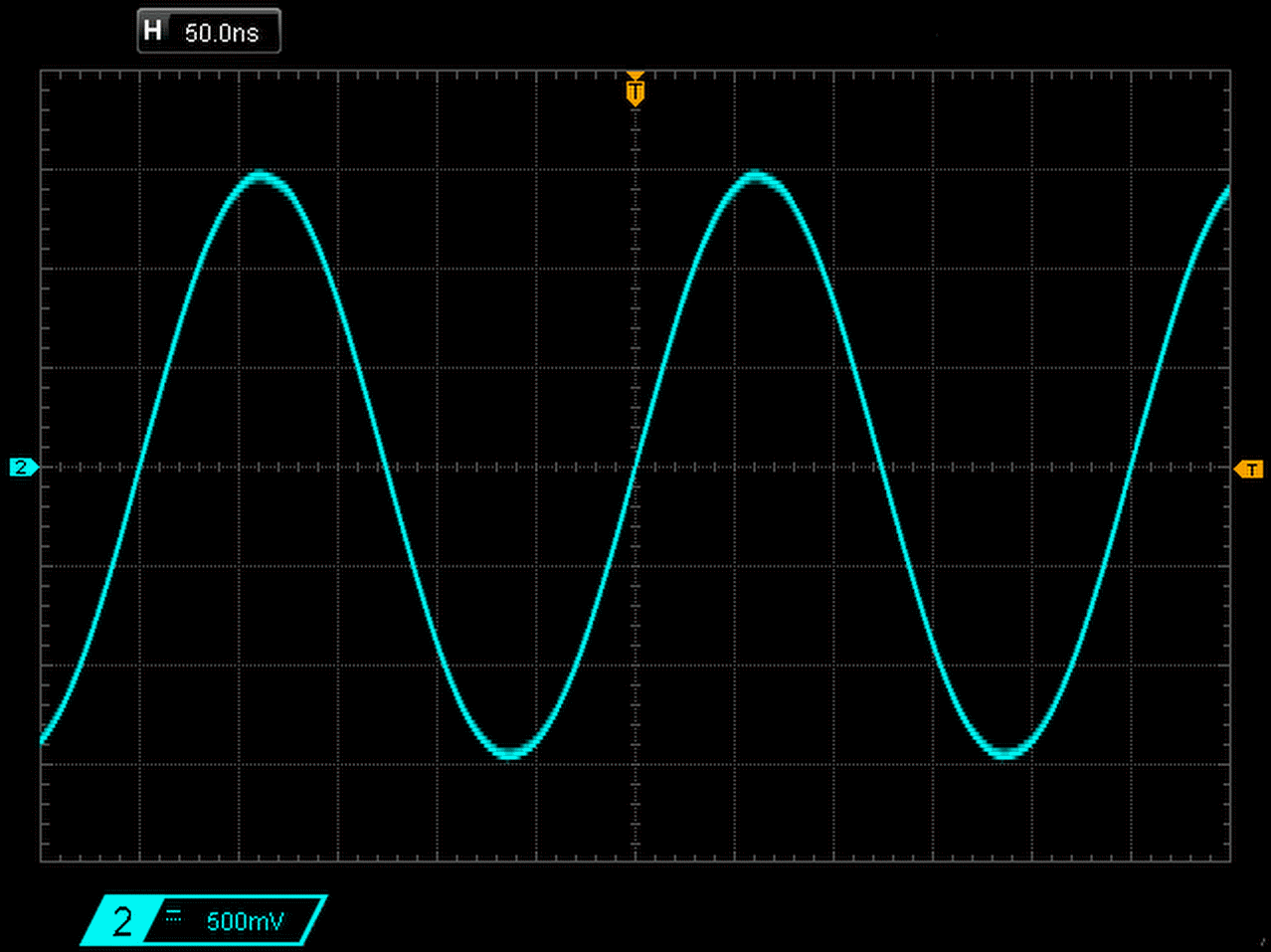
Wir können uns das als Koordinatensystem vorstellen und die Periodendauer ($T$) und die Amplitude ($\hat{U}$) ablesen. Im Beispiel ist eine Periode 5 Kästchen oder Skalenteile lang. Multipliziert mit $\qty{50,0}{\nano\second}$ pro Skalenteil ergibt das die Periodendauer $\qty{250,0}{\nano\second}$. Die Amplitude, also die größte Abweichung von der Nulllage, beträgt $\qty{1500}{\milli\volt}$ oder $\qty{1,5}{\volt}$, denn sie ist 3 Skaltenteile hoch und jeder Teil entspricht $\qty{500}{\milli\volt}$.
Für einfache Messungen haben viele digitale Oszilloskope eine AUTO-Taste. Wenn man sie drückt, werden einige Einstellungen automatisch vorgenommen und meistens erscheint ein stehendes Bild der angelegten Signale. Die Anzeige lässt ich in der Waagerechten verschieben. Ein Drehknopf mit dieser Funktion ist oft mit X-Position beschriftet. Zum Ablesen der Periodendauer schiebt man einen markanten Punkt wie einen Nulldurchgang auf eine senkrechte Linie des Gitters und zählt, wie viele Skalenteile einer Periode entsprechen.
Sobald die Periodendauer einer Schwingung bekannt ist, lässt sich daraus auch die Frequenz bestimmen. In der Klasse N haben wir bereits den qualitativen Zusammenhang kennengelernt: Die Frequenz gibt die Zahl der Schwingungen pro Sekunde an. Beträgt die Periodendauer eine Sekunde, so ergibt sich eine Frequenz von 1 Hz. Halbieren wir die Periodendauer auf eine halbe Sekunde, passen zwei Schwingungen in eine Sekunde – die Frequenz liegt dann bei 2 Hz.
In der Klasse E betrachten wir diesen Zusammenhang nun als Formel:
$f=\dfrac{1}{T}$ oder $T=\dfrac{1}{f}$
Die Frequenz in Hertz ist der Kehrwert der Periodendauer in Sekunden.
Das Signal in Abbildung EA-3.6.2 hat also die Frequenz
$f = \dfrac{1}{250\text{ ns}} = 4 \text{ MHz}$.
Manchmal werden Signale ungewollt verformt. Das geschieht zum Beispiel, wenn in einen Verstärker eine zu hohe Eingangsspannung eingespeist wird. Man sagt dann, der Verstärker ist übersteuert und sein Ausgangssignal verzerrt. Starke Verzerrungen wie in Abbildung EA-3.6.3 kann man mit einem Oszilloskop erkennen. Für die Beurteilung von Audio-Signalen im Amateurfunk reicht das meistens aus.
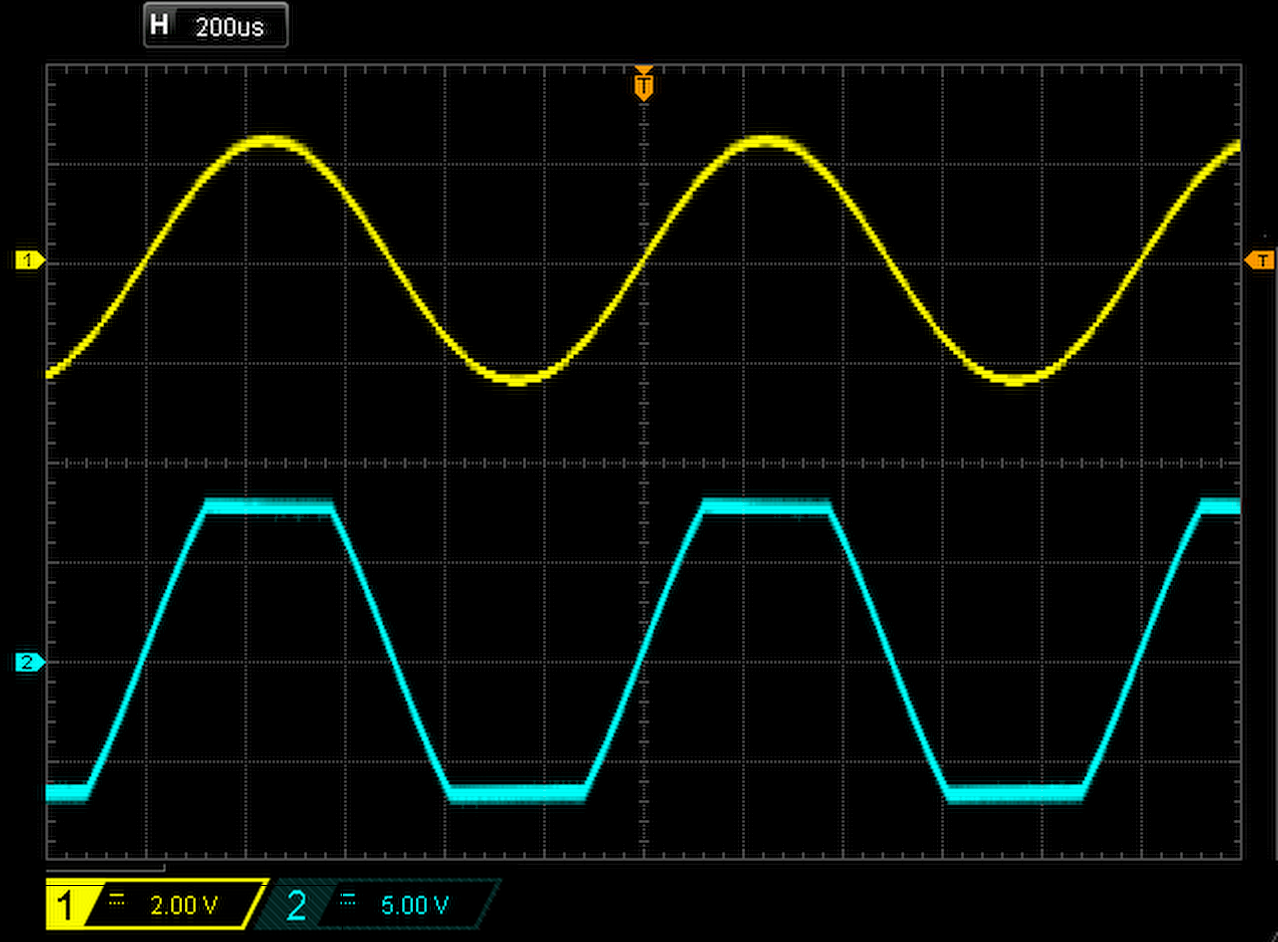
Ob ein Hochfrequenzsignal frei von Verzerrungen ist, die andere Frequenzbereiche beeinträchtigen, kann man mit einem Oszilloskop nicht gut genug einschätzen. Dafür ist ein Spektrum-Analysator das richtige Messgerät.