Wir stehen oft vor dem Problem, dass ein gewünschter Widerstandswert nicht in der sogenannten „Widerstands-Normreihe“ enthalten ist. Es könnte auch sein, dass ein Widerstand eine große Verlustleistung umsetzen muss, die in handelsüblichen Einzelwiderständen nicht möglich ist -- um nur zwei Beispiele zu nennen. Wir werden jetzt betrachten, wie wir durch Reihenschaltung oder Parallelschaltung von Widerständen andere Widerstandswerte erhalten können.
Alles, was wir wissen müssen, ist das Ohmsche Gesetz:
$U=R \cdot I$
(siehe Formelsammlung Seite 234 Mitte links – Stichwort: Ohmsches Gesetz)
| Wiederholung zum Widerstand |
| Schaltzeichen: siehe Abbildung 113 |
| Formelzeichen: R |
| Benennung des Widerstandes: $\Omega$ (Ohm) |
| Größenordnungen |
Zur Erinnerung:
| Vorsatz | Abkürzung | Wert |
| Pico | p | 10-12 = 0,000000000001 |
| Nano | n | 10-9 = 0,000000001 |
| Mikro | µ | 10-6 = 0,000001 |
| Milli | m | 10-3 = 0,001 |
| 100 = 1 | ||
| Kilo | k | 103 = 1000 |
| Mega | M | 106 = 1000000 |
| Giga | G | 109 = 1000000000 |
Das Bild zeigt zwei Widerstände $R_1$ und $R_2$, die hinter einander geschaltet werden. Sie vom gleichen Strom I durchflossen. An den Widerständen fallen dann die Spannungen
$U_1 = R_1 \cdot I$ und $U_2 = R_2 \cdot I$ ab.
Die Gesamtspannung $U_{ges}$ ist einfach die Summe dieser beiden Spannungen:
$U_{ges} = U_1 + U_2 = R_{ges} \cdot {I} = R_1 \cdot I + R_2 \cdot I$
Jetzt können wir den Widerstand berechnen, der zwischen den äußeren Klemmen zu sehen ist:
$R_{ges} = \dfrac{U_{ges}}{I} = R_1 + R_2$, weil sich auf beiden Seiten der Gleichung der Strom $I$ rauskürzt.
Das Ganze funktioniert auch bei mehr als zwei Widerständen:
$R_{ges} = R_1 + R_2 + R_3 + R_4 + ...$
(siehe Formelsammlung Seite 235 oben links – Stichwort: Widerstände in Reihenschaltung)

Knobelaufgabe:
Um eine
Die Belastbarkeit beträgt dann
Wie viele Widerstände sind notwendig und wie könnte die Schaltung aussehen?
(siehe auch Klasse A: Abschnitt Dummy-Load 2)



Doch wie verhält es sich, wenn wir zwei Widerstände $R_1$ und $R_2$ parallel schalten?
Jetzt liegt an beiden Widerständen die selbe Spannung $U$ an, die in den Widerständen die Ströme
$I_1 = \dfrac{U}{R_1}$ und $I_2 = \dfrac{U}{R_2}$
fließen lässt.
Der im äußeren Stromkreis fließende Strom ist die Summe dieser beiden Ströme:
$I_{ges} = I_1 + I_2 = \dfrac{U}{R_1} + \dfrac{U}{R_2}$
Wir suchen wieder einen Gesamtwiderstand $R_{ges}$, für den dann gelten muss: $I_{ges}=\dfrac{U}{R_{ges}}$ und folglich:
$\dfrac{1}{R_{ges}} = \dfrac{1}{R_1} + \dfrac{1}{R_2}$
Der Kehrwert des Gesamtwiderstands ist also die Summe der Kehrwerte der Einzelwiderstände. Eine Konsequenz ist, dass man bei einer Parallelschaltung einer Reihe gleicher Widerstände einfach den Wert des einzelnen Widerstands durch die Anzahl der Widerstände teilt.
Bei der Reihenschaltung ist die Wert des Gesamtwiderstands immer größer als der größte Einzelwiderstand. Bei der Parallelschaltung ist der Gesamtwiderstand immer kleiner als der kleinste Einzelwiderstand.
Auch hier können wir die Berechnung für beliebig viele parallele Widerstände durchführen:
$\dfrac{1}{R_{ges}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \dfrac{1}{R_4} + ...$
Den Ausdruck für zwei parallele Widerstände können wir nach den Regeln der Bruchrechnung auch schreiben als:
$R_{ges} = \dfrac{R_1 \cdot R_2}{R_1 + R_2}$
Bei der Parallelschaltung ist der Gesamtwiderstand immer kleiner als der kleinste Einzelwiderstand.
Betrachten wir ein praktisches Beispiel. Für das Testen von Sendern verwendet man gern eine Dummy Load, einen Widerstand, der die abgegebene Leistung in Wärme umsetzt. Für die meisten Senderausgänge muss diese Last einen Widerstand von etwa 50 $\Omega$ darstellen. Um aber auch etwas höhere Leistungen vertragen zu können, schaltet man geeignete Widerstände parallel.
Nehmen wir 10 Widerstände von 470 $\Omega$ mit je
$\dfrac{1}{R_{ges}} = \dfrac{10}{470\ \Omega}$ bzw.
$R_{ges}= \dfrac{470\ \Omega}{10} = 47\ \Omega$
was genau genug ist.
Genau darauf achten, dass die in der Rechnung verwendeten Widerstände immer die selben Einheiten haben. Ich empfehle immer, möglichst auf die Grundeinheit ($\Omega$) zu gehen. Schalten wir z.B. einen $1\ \text{k}\Omega$- und einen $10\ \Omega$-Widerstand in Reihe, dann rechnen wir $1000\ \Omega + 10\ \Omega = 1010\ \Omega$.
Einige der Aufgaben enthalten Widerstandsnetzwerke, in denen sowohl eine Reihen- als auch eine Parallelschaltung vorkommt. Da gehen wir so vor, dass wir erst z.B. die Parallelschaltung in einen äquivalenten Widerstand umwandeln, den wir dann mit dem in Reihe geschalteten dritten Widerstand zusammenfassen. Oder halt umgekehrt, je nach dem, was sich anhand des Schaltbildes anbietet.
Ein wichtiges Lösungsverfahren ist die „Methode des scharfen Hinsehens“ ... da gibt es zum Beispiel eine Schaltung, die einen Widerstand $R_1$ in Reihe mit zwei parallel geschalteten Widerständen $R_2$ und $R_3$ hat. Die Werte sind $R_1 = 1\ k\Omega$, $R_2 = 2000\ \Omega$ und $R_3 = 2\ k\Omega$. Nun sind aber $2\ k\Omega = 2000\ \Omega$. Die Paralellschaltung von $R_2$ und $R_3$ ergibt einen Widerstand, der halb so groß ist: $1000\ \Omega = 1\ k\Omega$. Den schalten wir in Reihe mit $R_1$ und erhalten das Ergebnis: $R_{ges}=2\ k\Omega$.
Der Taschenrechner kann stecken bleiben.
Bei Leistungsbetrachtungen geht man am Besten von dem bekannten Ausdruck für die Leistung aus:
$P = U \cdot I$
Bei der Reihenschaltung von z.B. drei gleichen Widerständen fließt durch alle Widerstände der gleiche Strom, aber an jedem einzelnen Widerstand fällt nur ein Drittel der äußeren Spannung ab. Bei der Parallelschaltung liegt an allen Widerständen die selbe Spannung, aber der Strom teil sich auf drei Pfade auf. In beiden Fällen verträgt also die Schaltung das dreifache der Leistung des einzelnen Widerstandes.
Lösung der Knobelaufgabe:
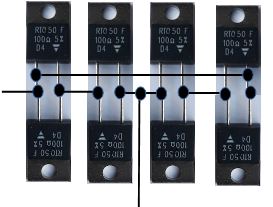
Variante 1: ((
(

Variante 2: (
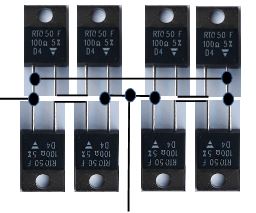
Variante 3: ((
(
Lösungshilfe:
ED 104:
ED 105:
ED 106:
ED 107:
ED 108:
ED 109:
ED 110:
ED 111:
ED 112:
ED 113:
| Formelsammlung auf Seite 234 |
| $U=R \cdot I$ |
| $I = \dfrac{U}{R}$ |
| Formelsammlung auf Seite 235 |
| $R_{ges} = R_1 + R_2 + R_3 + R_4 + ...$ |
| $\dfrac{1}{R_{ges}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \dfrac{1}{R_4} + ...$ |
| $R_{ges} = \dfrac{R_1 \cdot R_2}{R_1 + R_2}$ |
Zusammenfassung:
Formelsammlung auf Seite 234
$U=R \cdot I$
$I = \dfrac{U}{R}$
Formelsammlung auf Seite 235
$R_{ges} = R_1 + R_2 + R_3 + R_4 + ...$
$\dfrac{1}{R_{ges}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \dfrac{1}{R_4} + ...$
$R_{ges} = \dfrac{R_1 \cdot R_2}{R_1 + R_2}$