Im Amateurfunk haben wir es häufig sowohl mit sehr großen als auch mit sehr kleinen Zahlen zu tun. Die Einheit der Frequenz – das Hertz (Hz) – sowie die typischen Vorsätze für große Zahlen wie Kilo (k), Mega (M) und Giga (G) sind uns bereits begegnet.
Auch für kleine Zahlen gibt es solche Einheitenvorsätze. Bekannt ist zum Beispiel Milli, abgekürzt mit m. Ein Millimeter entspricht einem Tausendstel Meter, also 0,001 m. Die am meisten verwendeten Vorsätze für große und kleine Zahlen stehen in Tabelle 12.
| Vorsatz | Abkürzung | Wert |
| Pico | p | 10-12 = 0,000000000001 |
| Nano | n | 10-9 = 0,000000001 |
| Mikro | µ | 10-6 = 0,000001 |
| Milli | m | 10-3 = 0,001 |
| 100 = 1 | ||
| Kilo | k | 103 = 1000 |
| Mega | M | 106 = 1000000 |
| Giga | G | 109 = 1000000000 |
Neben den Einheiten Hertz und Meter, die wir bereits kennengelernt haben, gibt es noch viele weitere physikalische Einheiten, auf die wir im weiteren Verlauf des Kurses eingehen werden. Dazu gehören zum Beispiel die elektrische Spannung, gemessen in Volt (V), der elektrische Strom in Ampere (A), die Leistung in Watt (W), der elektrische Widerstand in Ohm (Ω) und weitere.
Um die folgenden Sachverhalte verstehen zu können, ist es noch nicht notwendig, diese Einheiten im Detail zu kennen. Wichtig ist zunächst nur, die Bedeutung und Anwendung der Einheitenvorsätze zu verstehen.
Leider kann man diese gezeigten Einheitenvorsätze nicht direkt in jeden Taschenrechner eingeben. Man verwendet dafür sogenannte Zehnerpotenzen.
Schauen wir uns das zunächst am Beispiel des Vorsatzes Kilo an, der für $1000$ steht: Statt $1000$ kann man auch $10 \cdot 10 \cdot 10$ schreiben. Dafür gibt es die Abkürzung $10^3$ (gesprochen „10 hoch 3“ oder „3. Potenz von 10“). Die Angaben
Man kann es sich auch anders merken: Man multipliziert die Zahl so oft mit 10, wie die Hochzahl (der Exponent) angibt. Bei Zahlen ohne Komma hängt man einfach so viele Nullen an, wie im Exponent steht.
Für eine Million muss man nicht drei, sondern sechs Exemplare der Zahl 10 miteinander multiplizieren. Also entspricht der Vorsatz Mega dem Wert $10^6$. Die Schreibweise $28 \cdot 10^6$ Hz bedeutet demnach dasselbe wie
Für kleine Zahlen funktioniert es ähnlich. Ein Tausendstel ist $\frac{1}{10}$ · $\frac{1}{10}$ · $\frac{1}{10}$. Das schreibt man als $10^{-3}$ („zehn hoch minus drei“). Der Wert $3,5\cdot 10^{-3}$ V ist also nichts anderes als $3,5$ mV und $22 \cdot 10^{-6}$ V steht für $22$ µV. Die wichtigsten Zehnerpotenzen stehen wieder in Tabelle 12.
Technisch-wissenschaftliche Taschenrechner verfügen in der Regel über eine Taste für Potenzen, meist bezeichnet mit $x^y$. Manche Modelle bieten zusätzlich eine vereinfachte Eingabemöglichkeit für Zehnerpotenzen: eine Taste mit der Beschriftung Exp, E oder $\cdot 10^x$. Diese steht für „mal zehn hoch …“ und erleichtert die Eingabe sehr großer oder sehr kleiner Zahlen.
Beispiel: Um den Wert $3,5 \cdot 10^6$ einzugeben, drückt man: 3.5 → Exp → 6
Schau am besten in die Bedienungsanleitung deines Taschenrechners, um die genaue Tastenkombination zu finden.
Die Anzeige besonders großer oder kleiner Werte hängt vom Gerät ab. Manche schreiben sie als gewöhnliche Zehnerpotenzen, andere mit Exp oder E für mal 10 hoch. Oft schaltet die Taste S/D zwischen verschiedenen Darstellungen um. In der Zehnerpotenz-Schreibweise verschieben Tasten wie ENG,
Abbildung 1 zeigt drei Darstellungen der selben Zahl in einer Taschenrechner-App. Die drei Buttons für den Umgang mit Zehnerpotenzen wurden rot markiert.
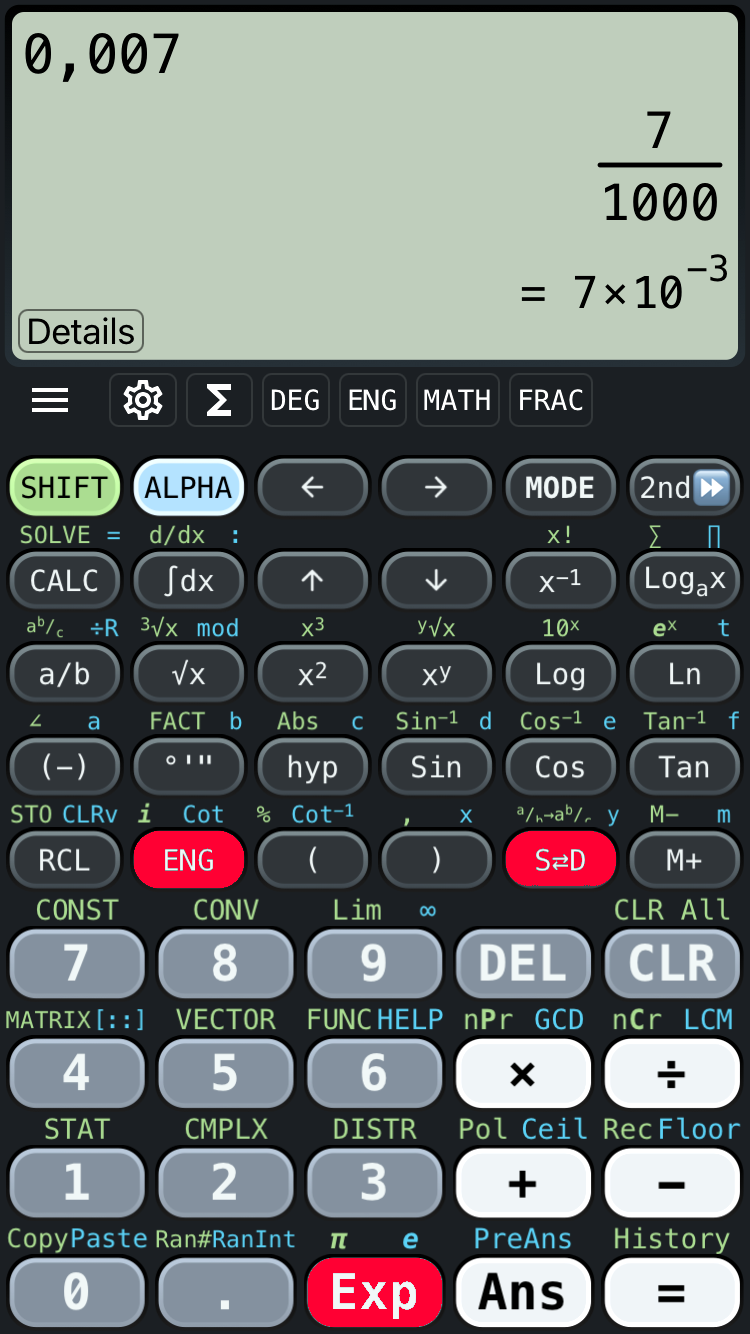
Im Folgenden findest du mehrere Prüfungsfragen, die du mithilfe deines Taschenrechners lösen kannst. Gib dazu die jeweilige Zahl entsprechend der Aufgabenstellung ein – achte dabei gegebenenfalls auf die Einheitenpräfixe und verwende den Exponentialmodus. Mit der ENG-Taste kannst du die Umrechnung automatisch durchführen lassen.
Mit etwas Übung lassen sich die Aufgaben natürlich auch im Kopf lösen. Die Einheiten können in diesen Beispielen vernachlässigt werden, da es hier in erster Linie auf die korrekte Darstellung in Exponentialschreibweise bzw. auf den passenden Einheitenpräfix ankommt. In zukünftigen Berechnungen wird es zunehmend wichtig sein, ein Ergebnis mit einem bestimmten Einheitenpräfix auszuwählen oder entsprechend umzurechnen.
