Reihen- und Parallelschaltung gemischter Bauelemente

In Parallelschwingkreisen werden Spulen und Kondensatoren kombiniert. Zur genauen Berechnung der Resonanzfrequenz, müssen „unsichtbare“ Kapazitäten, wie Wicklungskapazität und Schaltungskapazität, berücksichtigt werden. Die folgende Aufgabe beschreibt die wirksamen Kapazitäten sehr praxisnah.

AD103: Wie groß ist die Gesamtkapazität dieser Schaltung, wenn $C_1$ = 0,1 nF, $C_2$ = 1,5 nF, $C_3$ = 220 pF und die Eigenkapazität der Spule 1 pF beträgt?

1) Kurzbeschreibung: Schaltplan in rechteckiger Leitungsführung mit zwei Anschlusspunkten (oben und unten) und vier parallelen Zweigen: links ein Kondensator „C_1“, in der Mitte eine Spule, rechts ein Kondensator „C_2“ und ganz rechts ein Kondensator „C_3“.

2) Ausführliche Beschreibung: Der Schaltplan enthält einen rechteckigen Schaltkreis mit zwei Anschlusspunkten (oben und unten) und vier parallelen Zweigen, die oben und unten in Verzweigungspunkten zusammengeführt werden. Links ist ein Kondensator „C_1“ eingezeichnet, in der Mitte eine Spule, rechts davon ein Kondensator „C_2“ und ganz rechts ein Kondensator „C_3“.

Das Hauptproblem bei der Lösung der Aufgaben ist die Beachtung und Umwandlung der unterschiedlichen Vorsilben auf eine einheitliche, sinnvolle Vorsilbe, um nicht zu große oder zu kleine Zahlenwerte zu bekommen. Im Abschnitt „Kondensatoren in Reihen- und Parallelschaltung “ der Klasse E wurde dies schon ausführlich erklärt. Als gemeinsame Vorsilbe sollten bei der folgenden Frage alle Kapazitätswerte in Picofarad (pF) umgewandelt werden, da auch das Ergebnis in Picofarad angegeben ist. Die Eigenkapazität der Spule (Kapazität der Windungen gegeneinander) muss zusätzlich addiert werden.

Schwieriger ist die Berechnung einer Reihenschaltung von 3 Kondensatoren.

Bei der folgenden Aufgabe hat die kleinste Kapazität den Wert 22 pF. Die Gesamtkapazität muss deshalb kleiner als 22 pF sein. Da in der Lösung zwei Ergebnisse unter 22 pF zu finden sind, ist keine Abschätzung möglich, sondern es ist eine Rechnung notwendig.

$$\frac{ 1 }{ C_{ G } } = \frac{ 1 }{ C_{ 1 } } + \frac{ 1 }{ C_{ 2 } } + \frac{ 1 }{ C_{ 3 } }$$

(siehe Formelsammlung Seite 236 unten – Stichwort: Kondensatoren in Reihenschaltung )

AD101: Wie groß ist die Gesamtkapazität, wenn drei Kondensatoren $C_1$ = 0,10 nF, $C_2$ = 47 pF und $C_3$ = 22 pF in Reihe geschaltet werden?

Man gibt die Kapazitätswerte immer mit der 1/x – Taste in den Taschenrechner ein und muss am Schluss nochmals 1/x drücken.

C1 mit 0,1 nF muss in Picofarad umgewandelt werden. Dies ergibt 100 pF.

$$\frac{ 1 }{ C_{ G } } = \frac{ 1 }{ 100 } + \frac{ 1 }{47 } + \frac{ 1 }{22 }$$

AD104: Berechne den Betrag des Scheinwiderstands $Z$ für eine Reihenschaltung aus $R$ = 100 Ohm und $C$ = 1 nF bei 1 MHz.

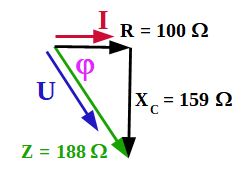
Der folgende Alt-Text wurde noch nicht geprüft: 1. Kurzzusammenfassung: Schematische Grafik mit farbigen Pfeilen und den Beschriftungen R = 100 Ω, X_C = 159 Ω, Z = 188 Ω sowie den Symbolen I, U und φ.

2. Detaillierte Beschreibung: Ein schwarzer Pfeil zeigt nach rechts und ist mit „R = 100 Ω“ beschriftet; an dessen Spitze hängt ein schwarzer Pfeil nach unten mit der Beschriftung „X_C = 159 Ω“. Vom gemeinsamen Startpunkt der Pfeile verläuft ein grüner Pfeil schräg nach rechts unten mit der Aufschrift „Z = 188 Ω“. Ein blauer Pfeil mit dem Buchstaben „U“ verläuft ebenfalls schräg nach rechts unten, etwas oberhalb bzw. mit kleinerem Neigungswinkel als der grüne Pfeil. Oben links zeigt ein roter Pfeil nach rechts, beschriftet mit „I“. Zwischen dem roten Pfeil „I“ und dem blauen Pfeil „U“ steht ein violettes φ, das den Winkel zwischen diesen beiden Pfeilen markiert. Die schwarzen Pfeile für R und X_C stehen zueinander rechtwinklig und bilden zusammen mit dem grünen Z-Pfeil ein Dreieck. — Abbildung A-4.5.1: Widerstandsdreieck für die Reihenschaltung von R und $X_C$

Das Widerstandsdreieck für die Reihenschaltung von R und $X_C$ veranschaulicht grafisch die Berechnung mit der Formel $|Z| = \sqrt{R^2 + {X_C}^2} = \sqrt{(100\Omega)^2 + (159\Omega)^2}$ Zusätzlich sieht man auch den Phasenverschiebungswinkel $\varphi$ zwischen U und I und das I voreilend ist.

Zur Berechnung eines Scheinwiderstandes benutzen wir die Formel

$$|Z| = \sqrt{R^2 + X^2}$$

(siehe Formelsammlung Seite 235 unten rechts – Stichwort: Wechselspannung -> Scheinwiderstand) Zur Anwendung dieser Formel muss der Blindwiderstand Xc des Kondensators bei 1 MHz zuerst berechnet werden. Die Formel für $X_{\textrm{C}}$ lautet:

$$X_{\textrm{C}} = \frac{1}{\omega \cdot C}$$

(siehe Formelsammlung Seite 236 unten links – Stichwort: Kapazität -> kapazitiver Blindwiderstand )

Bei der Eingabe der Bauteilwerte in den Taschenrechner müssen die Zehnerpotenzen sorgfältig hinzugefügt werden. 1 MHz = 1 x $10^6$ Hz; 1 nF = 1 x $10^{-9}$ F $X_C$ ergibt sich dann für den 1 nF Kondensator bei 1 MHz zu $159\Omega$. Nun kann der Scheinwiderstand |Z| berechnet werden.

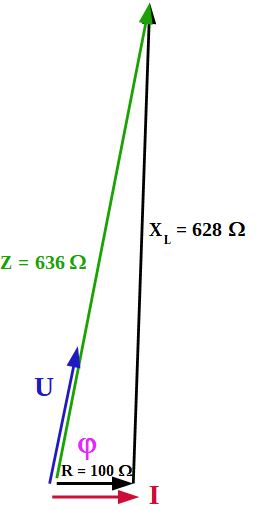
$$|Z| = \sqrt{R^2 + {X_C}^2}$$

AD105: Berechne den Betrag des Scheinwiderstands $Z$ für eine Reihenschaltung aus $R$ = 100 Ohm und $L$ = 100 μH bei 1 MHz.

Der Rechenweg ist der Gleiche wie vorher beschrieben und die Zehnerpotenzen sind wieder zu beachten: 100 µH = 100 x $10^{-6}$ H 1 MHz = 1 x $10^6$ Hz $X_{\textrm{L}}$ muss mit der Formel $X_{\textrm{L}} = \omega \cdot L$ zuerst berechnet werden, danach kann die Berechnung des Scheinwiderstandes |Z| mit der Formel $|Z| = \sqrt{R^2 + {X_L}^2}$ erfolgen.

Der folgende Alt-Text wurde noch nicht geprüft: 1) Kurze Zusammenfassung: Farbiges Vektordiagramm mit Pfeilen und Beschriftungen zu I, R = 100 Ω, X_L = 628 Ω, Z = 636 Ω, U und φ.

2) Detaillierte Beschreibung: Auf weißem Hintergrund starten mehrere Pfeile an einem gemeinsamen Punkt links unten. Ein roter Pfeil zeigt waagerecht nach rechts und ist mit I beschriftet; daneben steht in schwarz „R = 100 Ω“. Ein langer schwarzer Pfeil zeigt senkrecht nach oben und ist mit „X_L = 628 Ω“ beschriftet. Ein langer grüner Pfeil verläuft schräg nach oben rechts und trägt die Beschriftung „Z = 636 Ω“. Ein kurzer blauer Pfeil zeigt schräg nach oben, nahe dem Startpunkt, und ist mit „U“ gekennzeichnet. Direkt am Ursprung befindet sich in Magenta der griechische Buchstabe φ. Die Pfeile bilden optisch ein rechtwinkliges Dreieck aus horizontaler, vertikaler und schräger Komponente. — Abbildung A-4.5.2: Widerstandsdreieck für die Reihenschaltung von R und $X_L$

Das Widerstandsdreieck für die Reihenschaltung von R und $X_L$ veranschaulicht grafisch die Berechnung mit der Formel $|Z| = \sqrt{R^2 + {X_L}^2} = \sqrt{(100\Omega)^2 + (628\Omega)^2} $ Zusätzlich sieht man auch den Phasenverschiebungswinkel $\varphi$ zwischen U und I und das I nacheilend ist.

Lösungshilfe AD 103: 100 pF + 1500 pF + 220 pF + 1 pF = 1821 pF AD 101: 13 pF AD 104: $X_C$ = $ \frac{1}{{6,28 \cdot 1 \ {10^6} Hz} \cdot 1 \ 10^{-9}\ F}$ = 159 Ω

$$|Z| = \sqrt{R^2 + {X_C}^2} = \sqrt{(100\Omega)^2 + (159\Omega)^2} \approx 188\Omega$$

AD 105: 636 Ω

$$X_{\textrm{L}} = \omega \cdot L = 2 \cdot \pi \cdot f \cdot L = 2 \cdot \pi \cdot 1MHz \cdot 100\mu H = 628\Omega$$ $$|Z| = \sqrt{R^2 + {X_L}^2} = \sqrt{(100\Omega)^2 + (628\Omega)^2} \approx 636\Omega$$

Weiter zum nächsten Kapitel: Strom- und Spannungsversorgung