Spule II

In der Funktechnik spricht man auch von einer Impedanz. Beispiele: Antennenimpedanz bei 3,6 MHz, Eingangs- und Ausgangsimpedanz einer Verstärkerstufe, Impedanzwandler

Da die Gesamtspannung an Z anliegt und der Strom in Phase mit R zu sehen ist, ergibt sich eine Phasenverschiebung von $phi$ = 45 Grad, wobei I gegenüber U nacheilend ist.

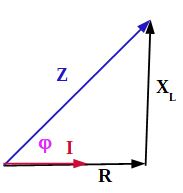
Bei einer Reihenschaltung von Blindwiderstand und Wirkwiderstand ergibt sich ein Scheinwiderstand Z, der nur im Betrieb an Wechselspannung auftritt und nicht mit einem Ohm-Meter gemessen werden kann. Er wird auch als Impedanz Z bezeichnet und als Widerstand in Ohm angegeben. Merke: Der Begriff Impedanz steht für einen Widerstand, der sich aus einem ohmschen Anteil (R) und einem kapazitiven ($X_C$) und/oder induktiven Anteil ($X_L$) zusammensetzt.

Beispiel: Wirkwiderstand 100 Ω und Blindwiderstand 100 Ω in Reihenschaltung ergeben einen Scheinwiderstand (Impedanz) von 141 Ω. Das Ergebnis entsteht durch geometrische Addition der beiden Widerstände über ein rechtwinliges Dreieck nach dem den Satz des Pythagoras. $a^2$ +$b^2$ = $c^2$ Für die Widerstände bedeutet dies: $R^2$ +$X_L ^2$ = $Z^2$ $Z = \sqrt{{100^2} + {100^2}} $ = 141 Ω Bitte nachrechnen!

In der Funktechnik ist vor allem das Verhalten an Wechselspannung wichtig. Die Spule zeigt, ähnlich wie ein Kondensator, einen „Wechselstromwiderstand “, dass heißt, obwohl der Spulendraht nur einen sehr kleinen ohmschen Widerstand (Leiterwiderstand) besitzt, fließt bei einem Betrieb an Wechselspannung kein Kurzschlussstrom, sondern ein Strom, der mit steigender Frequenz der Wechselspannung kleiner wird.

Die Ursache ist der Anstieg des induktiven Blindwiderstandes $X_L$.

(siehe Formelsammlung Seite 236 oben links – Stichwort: Induktiver Blindwiderstand) $X_L$" links oben.

$$X_L =\omega * L = 2 * \pi * f * L$$

Beispielrechnung für die Frage AC 204: $X_L$ = 2 *$ \pi$ * 100 MHz * 3 µH Jetzt werden die Vorsilben in Zehnerpotenzen umgewandelt, damit das Ergebnis in Ohm berechnet werden kann. $X_L$ = $6,28 * 100 *10^6 * 3 * 10^{-6}$ Ohm Die Zehnerpotenzen $10^6 * 10^{-6}$ ergeben 1. Im letzten Schritt werden die verbliebenen Zahlen multipliziert. $X_L$ = 6,28 * 100 * 3 = 1884 Ω

Mit einem vektoriellen Network Analyzer (VNA) läßt sich die Veränderung des induktiven Blindwiderstandes $X-L$ in Abhängigkeit von der Frequenz darstellen. Wir sprechen auch hier von einem Blindwiderstand, da eine verlustfreie Spule keine Wirkenergie aufnimmt. Sollte eine Spule bei Hochfrequenzanwendungen warm werden, dann besitz sie Verluste, die diese Erwärmung bewirken. Die Verluste entstehen durch den ohmschen Widerstand des Drahtes und zusätzlich wirkt auch noch der Skin-Effekt, der den Drahtquerschnitt scheinbar verkleinert.

Die rote Linie zeigt die Phasenlage des induktiven Blindwiderstandes $X_L$.

Die Phasenverschiebung zwischen Spannung und Strom beträgt 90 Grad, wobei der Strom nacheilend ist. Daraus ergibt sich eine Leistungskurve, die um die Nulllinie symmetrisch schwankt. Der Mittelwert ergibt Null, d. h. es wird keine Wirkleistung aufgenommen. Wir sprechen deshalb auch bei einer verlustfreien Spule von Blindleistung und Blindwiderstand.

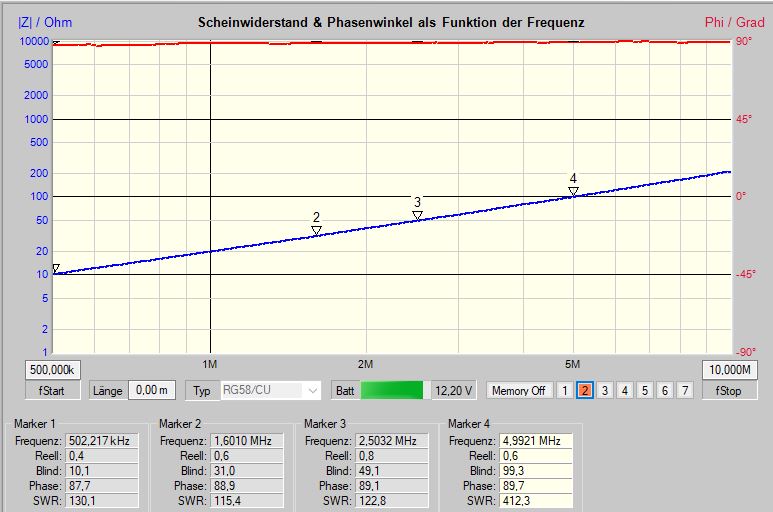
Sollte eine Spule bei Hochfrequenzanwendungen warm werden, dann besitzt sie Verluste, die diese Erwärmung bewirken. Die Verluste entstehen durch den ohmschen Widerstand des Drahtes und zusätzlich wirkt auch noch der Skin-Effekt, der den Drahtquerschnitt scheinbar verkleinert.

Grundsätzlich steigt die Induktivität wenn die Windungszahl erhöht wird, die Spulenlänge verkürzt wird, die Querschnittsfläche der Spule vergrößert wird und ein magnetisch leitfähigeres Material als Spulenkern verwendet wird. Zur Erhöhung der Induktivität, ohne die Windungszahl drastisch zu steigern, wird die Wicklung auf einen Ferritringkern gewickelt. Drosselspulen mit hoher Induktivität werden zur Verringerung hochfrequenter Ströme eingesetzt.

Eine wichtige Kenngöße einer Spule ist die Induktivität L. Sie gibt an, welche Selbstinduktionsspannung die Spule erzeugen kann und dadurch den fließenden Strom, im Einschalt- und Ausschaltmoment verzögert. Der Formelbuchstabe L wurde zu Ehren des Professors Emil Lenz aus St. Petersburg (1804 – 1864, Verfasser der Lenzschen Regel) gewählt.

Bei Ringkernspulen wird zur Erleichterung der Induktivitätsberechnung ein sogenannter $A_L$-Wert des Kernmaterials angegeben. Die Berechnung der Induktivität lautet dann: L = $N^2$ * $A_L$ (siehe Formelsammlung Seite 236 oben rechts – Stichwort: Induktivität einer Ringkernspule) ACHTUNG: Die Benennung des $A_L$-Wertes ist in Nanohenry pro Windungen im Quadrat angegeben. Berechnungsbeispiel für die Induktivität einer Ringkernspule Frage AC 205: L = $N^2$ * $A_L$ L = $14^2$ * 1,5 nH = 294 nH = 0,294 µH Die letzte Umwandlung ist notwendig, da die Lösung mit dieser Vorsilbe angegeben ist.

Beispielrechnung für die Frage AC 207: Berechnungsbeispiel für die Windungszahl einer Ringkernspule:

$$N = \sqrt \frac{L}{A_L}$$ $$N = \sqrt \frac{2 \ {mH}}{250 \ { nH} }$$

Wichtig: Umwandlung von 2 mH in 2 000 000 nH, damit sich gleiche Vorsilben kürzen lassen.

$$N = \sqrt \frac{2000 000 \ {nH} }{250 \ {nH} }$$ $$N = \sqrt {8000}$$ $$N = 89,4$$

Man wird 90 Windungen aufbringen.

*Zusammenfassung (Version 1)*: Impedanz = besteht aus Wirkwiderstand und Blindwiderstand = Scheinwiderstand in Ohm

MERKE: Induktivitäät, Strom zu späät!

Formel Seite 236

$$X_L =\omega * L = 2 * \pi * f * L$$

Umgestellt nach L:

$$L =\frac{X_L}{2\pi \cdot f}$$

$A_L$ – Wert in nH !!! L = $N^2$ * $A_L$ Umgestellt nach N:

$$N = \sqrt \frac{L}{A_L}$$

Hohe Spulenverluste = niedrige Güte = großer tan „delta“ = großer ESR

Hier geht es um die Abschirmung des elektrischen Feldes durch ein Alu-Gehäuse.

Zur Abschirmung eines Magnetfeldes benötigt man ein magnetisch gut leitfähiges Material.